Question

Rain is falling vertically with a velocity of \[25m{s^{ - 1}}\]. A woman rides a bicycle with a speed of \[10m{s^{ - 1}}\] in the north to south direction. What is the direction (angle with vertical) in which she should hold her umbrella to save herself from rain?
A) ${\tan ^{ - 1}}\left( {0.4} \right)$
B) ${\tan ^{ - 1}}\left( 1 \right)$
C) ${\tan ^{ - 1}}\left( {\sqrt 3 } \right)$
D) ${\tan ^{ - 1}}\left( {2.6} \right)$

Answer 1

Hint: In the given question, we have the velocity of the rain and the velocity of the woman with which she is riding a bicycle in the north to south direction. With this information, we can find the velocity of rain with respect to the woman. Now, the relative velocity will be forming an angle with the vertical which can then be calculated by the tangent of the angle by using the direction diagram.

Complete step by step solution:
According to the question, we are given:
Velocity of rain, \[{v_R} = 25m{s^{ - 1}}\]
Velocity of woman, \[{v_W} = 10m{s^{ - 1}}\]
Now, we need to calculate the relative velocity.
Velocity of rain with respect to the woman will be given by:
\[{v_{R/W}} = {v_R} - {v_W}\]
Let us now see the direction diagram to find the angle with the vertical.


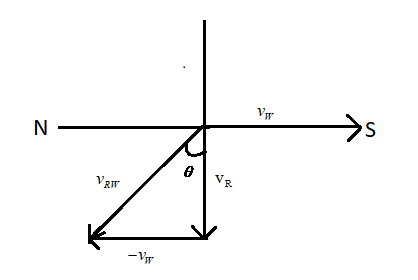
Now, the relative velocity ${v_{R/W}}$ is making an angle $\theta $ with the vertical axis.
From the above diagram, we can find the basic elements which are:
The perpendicular of the triangle formed is \[{v_W}\] and the base of the triangle is \[{v_R}\].
So, we can calculate the tangent of the angle by dividing the perpendicular by the base of the triangle.
\[
  \tan \theta = \dfrac{{{v_W}}}{{{v_R}}} = \dfrac{{10}}{{25}} = 0.4 \\
  \theta = {\tan ^{ - 1}}\left( {0.4} \right) \\
 \]
Therefore, the woman should hold her umbrella at an angle of \[\theta = {\tan ^{ - 1}}\left( {0.4} \right)\] with the vertical towards the south.

Hence, option (A) is correct.

Note: These types of questions can be solved by using basic mathematics with the help of a direction diagram. We should always be cautious in doing such calculations because a small calculation mistake can lead us to incorrect answers. Also, we need to be precise with the details given in the question.