Question

Prove that the locus of the middle point of a portion of a normal intersected between the curve and the axis is a parabola whose vertex is the focus and whose latus rectum is one quarter of the original parabola.

Answer 1

Hint: The equation of normal in parametric form is given as \[y=-tx+2at+a{{t}^{3}}\], where the normal is drawn at a point \[P\] with parameter \[t\].

First of all , let’s take the equation of the parabola to be \[{{y}^{2}}=4ax\].


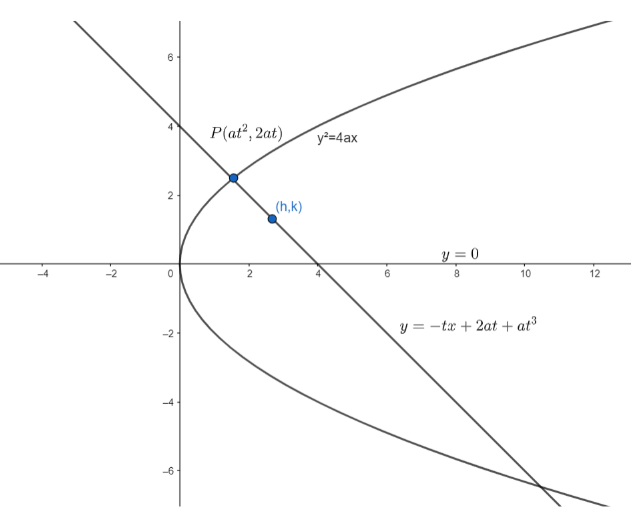
Coordinates of any point on the parabola in parametric form is given as \[P\left( a{{t}^{2}},2at \right)\].
We know, equation of normal in parametric form , where the normal is drawn at a point \[P\] with parameter \[t\], is given as
\[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Also, the equation of axis of the parabola is
\[y=0.....\left( ii \right)\]
To find the points of intersection of \[\left( i \right)\]and\[\left( ii \right)\], we substitute \[y=0\] in \[\left( i \right)\].
So, \[0=-tx+2at+{{t}^{3}}\]
\[\Rightarrow x=2a+a{{t}^{2}}\]
So , the point of intersection of the axis and the normal is \[\left( 2a+a{{t}^{2}},0 \right)\].
Now , let the midpoint of intercepted portion be \[\left( h,k \right).....\left( iii \right)\]
But we also know that the extremities of the intercepted portion are \[\left( a{{t}^{2}},2at \right)\] and \[\left( 2a+a{{t}^{2}},0 \right)\].
Now, we know that the coordinates of the midpoint of the line joining two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given as: \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
So, the coordinates of the midpoint are
\[\left( \dfrac{a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{2at+0}{2} \right)\]
\[=\left( a{{t}^{2}}+a,at \right)...\left( iv \right)\]
So, from \[\left( iii \right)\]and \[\left( iv \right)\], we can say
\[h=a{{t}^{2}}+a....\left( v \right)\], \[k=at\]
Now, \[k=at\]\[\Rightarrow t=\dfrac{k}{a}...\left( vi \right)\]
Substituting \[t=\dfrac{k}{a}\]in \[\left( v \right)\], we get
\[h=a{{\left( \dfrac{k}{a} \right)}^{2}}+a\]
\[\Rightarrow h=\dfrac{{{k}^{2}}}{a}+a\]
\[\Rightarrow {{k}^{2}}=ah-{{a}^{2}}........\] equation\[(vii)\]
Now , to get the equation of the locus of \[\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[\left( h,k \right)\] in equation\[(vii)\].
Or, \[{{y}^{2}}=a\left( x-a \right)....\left( viii \right)\] is the equation of the locus.
Now , we know the length of the latus rectum of \[{{y}^{2}}=4ax\] is \[4a\].
Now , the length of latus rectum of parabola given by equation \[\left( vii \right)\]is \[4\times \dfrac{a}{4}=a\]
Also, the vertex of \[\left( viii \right)\] is \[\left( a,0 \right)\] which is the focus of \[{{y}^{2}}=4ax\]
Hence , the length of the latus rectum of the locus is one quarter of the original parabola and the vertex of the locus is the focus of the original parabola .

Note: Length of latus rectum of parabola \[{{y}^{2}}=4ax\] is equal to \[4a\] and not \[a\].
Focus of parabola \[{{y}^{2}}=4ax\] is \[\left( a,0 \right)\] and not \[(4a,0)\].
Students generally get confused and make mistakes which results in wrong answers. So , such mistakes should be avoided .