Question

Prove that locus of the midpoint of a normal chord of the parabola \[{{y}^{2}}=4ax\] is \[{{y}^{4}}-2a(x-2a){{y}^{2}}+8{{a}^{4}}=0\]

Answer 1

Hint: Write the equation of the normal chord of the parabola in parametric form and apply the condition which relates the coordinates of the points at which the normal intersects the parabola. Find the midpoint of the points of intersection of normal to the parabola and solve it to get the locus of the parabola.

Complete step by step answer:
Let us consider a parabola \[{{y}^{2}}=4ax\]
We want to find the locus of midpoint of the normal chord of the parabola.

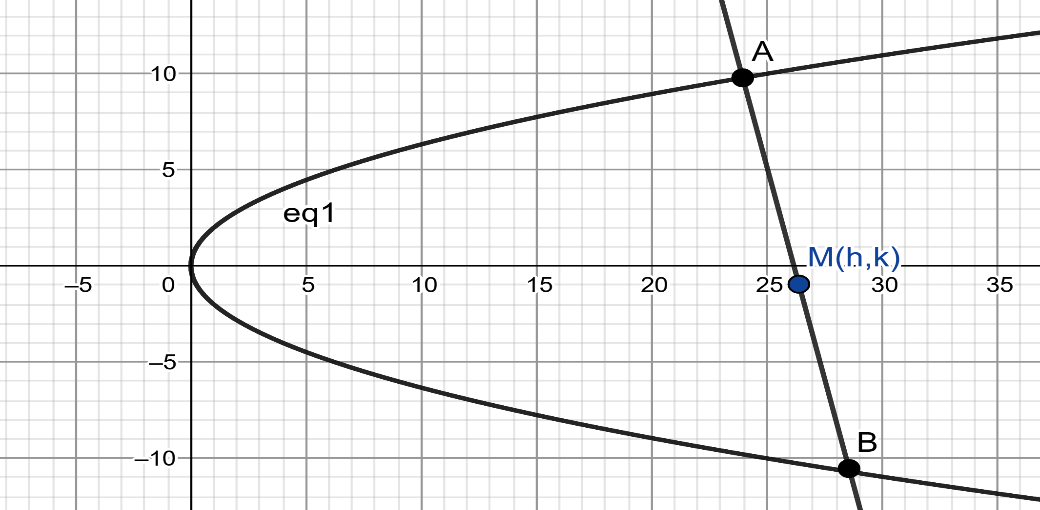
Let us consider the chord \[AB\] whose coordinates are of the form \[A(at_{1}^{2},2a{{t}_{1}})\] and \[B(at_{2}^{2},2a{{t}_{2}})\] , where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.
When a chord intersects normally to the parabola then the relation between the parameters of intersection points is \[{{t}_{2}}=-\dfrac{2}{{{t}_{1}}}-{{t}_{1}}\] .
Substituting the above equation in the coordinates of point \[B(at_{2}^{2},2a{{t}_{2}})\] , we get \[B\left( a{{\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)}^{2}},2a\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right) \right)\] .
We know that the midpoint of any two points of the form \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] .
Substituting \[{{x}_{1}}=at_{1}^{2},{{y}_{1}}=2a{{t}_{1}},{{x}_{2}}=at_{2}^{2},{{y}_{2}}=2a{{t}_{2}}\] in the above equation, we get \[\left( \dfrac{at_{1}^{2}+a{{\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)}^{2}}}{2},\dfrac{2a{{t}_{1}}+2a\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)}{2} \right)\] as the midpoint of chord \[AB\] .
Let’s assume that the midpoint of the chord \[AB\] is of the form \[\left( x,y \right)\] .
Thus, we have \[x=\dfrac{at_{1}^{2}+a{{\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)}^{2}}}{2},y=\dfrac{2a{{t}_{1}}+2a\left( -\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)}{2}\] .
Solving the above equation, we have \[x=\dfrac{a}{2}\left( t_{1}^{2}+\dfrac{4}{t_{1}^{2}}+t_{1}^{2}+4 \right)\] and \[y=\dfrac{2a}{2}\left( {{t}_{1}}-\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)\] .
Thus, we have \[y=\dfrac{2a}{2}\left( {{t}_{1}}-\dfrac{2}{{{t}_{1}}}-{{t}_{1}} \right)=\dfrac{-2a}{{{t}_{1}}}\] .
Rewriting the above equation, we have \[{{t}_{1}}=-\dfrac{2a}{y}\] .
Substituting the value \[{{t}_{1}}=-\dfrac{2a}{y}\] in the equation \[x=\dfrac{a}{2}\left( t_{1}^{2}+\dfrac{4}{t_{1}^{2}}+t_{1}^{2}+4 \right)\] , we have \[x=\dfrac{a}{2}\left( {{\left( -\dfrac{2a}{y} \right)}^{2}}+\dfrac{4}{{{\left( -\dfrac{2a}{y} \right)}^{2}}}+{{\left( -\dfrac{2a}{y} \right)}^{2}}+4 \right)\] .
Further simplifying the equation, we get \[x=\dfrac{a}{2}\left( \dfrac{4{{a}^{2}}}{{{y}^{2}}}+\dfrac{4}{\dfrac{4{{a}^{2}}}{{{y}^{2}}}}+\dfrac{4{{a}^{2}}}{{{y}^{2}}}+4 \right)\] .
By taking LCM and simplifying the terms, we get \[x=\left( \dfrac{4{{a}^{3}}}{{{y}^{2}}}+\dfrac{{{y}^{2}}}{2a}+2a \right)\]
   \[\Rightarrow x=\dfrac{8{{a}^{4}}+{{y}^{4}}+4{{a}^{2}}{{y}^{2}}}{2a{{y}^{2}}}\]
   \[\Rightarrow 2ax{{y}^{2}}=8{{a}^{4}}+{{y}^{4}}+4{{a}^{2}}{{y}^{2}}\]
   \[\Rightarrow 8{{a}^{4}}+{{y}^{4}}+4{{a}^{2}}{{y}^{2}}-2ax{{y}^{2}}=0\]
   \[\Rightarrow {{y}^{4}}-2a\left( x-2a \right){{y}^{2}}+8{{a}^{4}}=0\]
Hence, the locus of midpoint of normal chord of the parabola is \[{{y}^{4}}-2a\left( x-2a \right){{y}^{2}}+8{{a}^{4}}=0\] .
Note: We can write the equation of normal of the parabola in slope form and find the point of intersection of normal with the parabola and find the midpoint to get the locus of the parabola.