




How Do Waves Behave When They Hit a Surface?
Reflection and transmission of waves describe the behavior of waves when they encounter a boundary separating two different media. This topic is essential in understanding wave propagation, especially for mechanical waves on a string and other physical systems, and is frequently assessed in exams like JEE.
Fundamentals of Waves and Their Types
A wave is defined as a disturbance that transfers energy and momentum from one location to another without the transfer of matter. Mechanical waves, such as those on a string, require a material medium, while non-mechanical waves do not.
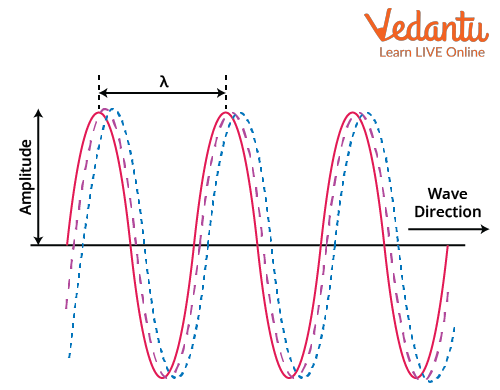
Sinusoidal waves are a fundamental class of waves characterized by oscillations that are mathematically described by sine or cosine functions of time and position within the medium.
Mathematical Description of Sinusoidal Waves
The general equation for a sinusoidal travelling wave moving towards the right is given by $y = A \cos(kx - \omega t)$, where $A$ is the amplitude, $k$ is the wave number, and $\omega$ is the angular frequency.
The wavelength $\lambda$ represents the spatial period of the wave, and the relationship between wave speed, frequency $f$, and wavelength is $v = \lambda f$. The wave number is $k = \dfrac{2\pi}{\lambda}$, and the angular frequency is $\omega = 2\pi f$.
Reflection and Transmission at a Boundary
When a travelling wave encounters a boundary between two media with different properties, part of the incident wave energy is reflected back into the original medium, and part is transmitted into the second medium.
The extent of reflection and transmission depends on the properties of the media, specifically their linear mass densities and the tension in the string. This scenario occurs in wave motion studies and is crucial for understanding the differences between reflection and refraction.
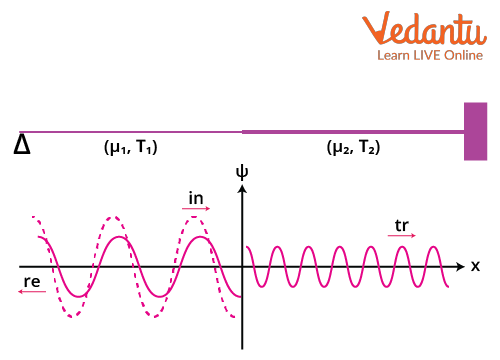
Wave Propagation on Joined Strings
Consider two semi-infinite strings of different linear mass densities $\mu_1$ and $\mu_2$ joined at $x = 0$, both under the same tension $T$. When an incident wave reaches the junction, it generates reflected and transmitted waves at this boundary.
The velocity of wave propagation in each string is determined by $v_1 = \sqrt{\dfrac{T}{\mu_1}}$ and $v_2 = \sqrt{\dfrac{T}{\mu_2}}$. The frequencies of all three waves remain identical, but wavelengths and wave numbers may differ in the two media.
A detailed analysis of such behavior supports deeper concepts in Wave Motion and boundary conditions.
Boundary Conditions at the String Junction
For physical continuity, two boundary conditions must be met at $x = 0$. The displacement of the string must be continuous across the junction, and the transverse force on the junction must also be continuous.
Mathematically, these conditions are expressed as: $y_1(0, t) = y_2(0, t)$ and $\left( \dfrac{\partial y_1}{\partial x} \right)_{x=0} = \left( \dfrac{\partial y_2}{\partial x} \right)_{x=0}$ where $y_1$ represents the sum of the incident and reflected wave displacements on string 1, and $y_2$ represents the transmitted wave displacement on string 2.
Formulating the Waves at the Boundary
The incident, reflected, and transmitted wave equations can be written as:
$y_{\text{in}} = A_{\text{in}} \cos(k_1 x - \omega t)$
$y_{\text{r}} = A_{\text{r}} \cos(k_1 x + \omega t)$
$y_{\text{t}} = A_{\text{t}} \cos(k_2 x - \omega t)$
Here, $k_1$ and $k_2$ are the wave numbers in strings 1 and 2, respectively. Substituting these into the boundary conditions yields a system of equations relating reflection and transmission amplitudes.
Derivation of Reflection and Transmission Coefficients
From the boundary conditions, the following linear equations are derived:
$A_{\text{in}} + A_{\text{r}} = A_{\text{t}}$
$k_1 A_{\text{in}} - k_1 A_{\text{r}} = k_2 A_{\text{t}}$
The reflection coefficient $R$ and transmission coefficient $T$ are defined as:
$R = \dfrac{A_{\text{r}}}{A_{\text{in}}}$, $T = \dfrac{A_{\text{t}}}{A_{\text{in}}}$
Solving these equations, we obtain: $R = \dfrac{k_1 - k_2}{k_1 + k_2}$, $T = \dfrac{2k_1}{k_1 + k_2}$
These expressions describe the amplitude ratios for reflected and transmitted waves at the boundary. Additional details on refraction and boundaries can be studied with the Refraction of Light Through Prism resource.
Summary Table: Key Wave Parameters
| Parameter | Expression |
|---|---|
| Wave speed in string ($v$) | $\sqrt{\dfrac{T}{\mu}}$ |
| Wave number ($k$) | $\dfrac{2\pi}{\lambda}$ |
| Reflection coefficient ($R$) | $\dfrac{k_1 - k_2}{k_1 + k_2}$ |
| Transmission coefficient ($T$) | $\dfrac{2k_1}{k_1 + k_2}$ |
| Wave equation | $y = A \cos(kx \pm \omega t)$ |
Physical Interpretation and Special Cases
When the second medium is denser than the first ($\mu_2 > \mu_1$), a phase inversion occurs in the reflected wave. When moving from a denser to a rarer medium, the reflected wave does not experience inversion.
For complete reflection ($\mu_2 \to \infty$), the transmission coefficient $T \rightarrow 0$ and reflection coefficient $R \rightarrow -1$, indicating total reflection with a phase change. Such behavior forms the basis for understanding Stationary Waves.
Applications and Simulations
Reflection and transmission of waves are fundamental in various physical systems. They are observed in acoustics, optics, and electromagnetic wave propagation. Simulations and visualizations, such as reflection and transmission of waves gifs, aid in conceptual understanding.
Study of wave behavior at boundaries is also critical in understanding Huygens Principle and wavefront propagation.
Important Points on Reflection and Transmission of Waves
- Boundary conditions determine reflection and transmission coefficients
- Frequency remains continuous at the boundary
- Amplitude changes depend on medium parameters
- Wave inversion occurs on reflection from denser media
- Total reflection arises with infinite impedance difference
Conclusion on Wave Reflection and Transmission
The reflection and transmission of waves at a boundary are governed by the physical properties of the media involved and continuity requirements at the boundary. These principles are essential for analyzing wave motion in strings, acoustics, and optics.
A thorough understanding of the reflection and transmission formulas, their derivations, and implications is vital for solving JEE-level problems involving waves and their boundaries. For an in-depth study, consult additional resources such as those on Polarized Light.
FAQs on Understanding Reflection and Transmission of Waves
1. What is meant by reflection and transmission of waves?
Reflection of waves occurs when a wave strikes a boundary and bounces back, while transmission happens when part of the wave passes through the boundary into a different medium.
Key points include:
- Reflection obeys the law of reflection: angle of incidence equals angle of reflection.
- Transmission may involve change in speed and direction, causing refraction.
- Energy splits between reflected and transmitted waves depending on material properties.
2. What are the laws of reflection of a wave?
The laws of reflection of a wave state that the angle of incidence is equal to the angle of reflection, and the incident wave, reflected wave, and normal all lie in the same plane.
- Angle of incidence = Angle of reflection
- All rays and normal are coplanar
- Valid for all types of mechanical and electromagnetic waves
3. What is meant by transmission of a wave?
Transmission of a wave refers to the process where a wave passes through a boundary between two media, entering the second medium.
During transmission:
- Part of the wave energy continues into the new medium
- The wavelength and speed may change depending on properties
- Some energy may be reflected or absorbed
4. What happens when a wave travels from one medium to another?
When a wave moves from one medium to another, it experiences partial reflection and partial transmission.
- Some energy is reflected back in the original medium
- Some is transmitted into the new medium, possibly with a speed and wavelength change
- The amplitude of reflected and transmitted waves is determined by the difference in properties of the two media
5. What is the difference between reflection and transmission of waves?
Reflection occurs when waves bounce off a surface, while transmission refers to waves passing through a boundary into a new medium.
- Reflection: Wave reverses direction at boundary, stays in same medium
- Transmission: Wave continues into different medium, may change speed and direction
- Both processes can occur simultaneously at a boundary
6. What is partial reflection and partial transmission of a wave?
Partial reflection and transmission mean that a wave striking a boundary will have some of its energy reflected and some transmitted.
- Not 100% reflected or transmitted
- Depends on difference in density and impedance of two media
- Common in sound and light waves, as well as mechanical waves on strings
7. What factors affect the reflection and transmission of waves?
The main factors influencing reflection and transmission of waves are the properties of the media and the angle of incidence.
- Impedance mismatch between two media
- Frequency and wavelength of the wave
- Nature of the boundary (rigid, free, fixed, loose)
8. Explain what happens when a wave is incident on a fixed end and a free end.
At a fixed end, a wave reflects with an inverted phase; at a free end, it reflects without phase inversion.
- Fixed end: Reflected wave is inverted (π phase shift)
- Free end: Reflected wave is upright (no phase shift)
9. What are practical examples of wave reflection and transmission in daily life?
Common examples of reflection and transmission of waves are seen in light, sound, and earthquakes.
- Echoes (sound reflection)
- Mirrors (light reflection)
- Glass windows (light transmission)
- Seismic waves (reflected/transmitted in earth's layers)
10. Why does the amplitude of a transmitted wave decrease after passing through a boundary?
The amplitude of a transmitted wave decreases because some energy is reflected or absorbed at the boundary.
- Energy conservation requires split between reflected and transmitted parts
- The greater the difference in medium properties, the lower the transmitted amplitude
11. What is the phase change on reflection of waves at a boundary?
When a wave reflects at a fixed boundary, it undergoes a phase change of π (inverted), but at a free boundary, there is no phase change.
- Fixed boundary: 180° phase change
- Free boundary: No phase change
12. State the conditions for total transmission and total reflection of waves.
Total transmission occurs when the two media have similar properties, while total reflection occurs when there is a complete mismatch (e.g., rigid barrier).
- Total transmission: No change in impedance, no reflection
- Total reflection: Complete mismatch (e.g., fixed boundary)
























