




How to Calculate the Rotational Kinetic Energy with Formula and Examples
The kinetic energy of a rotating body is a fundamental concept in rotational mechanics and is essential for understanding the energy associated with rotational motion. It quantitatively describes the energy due to the rotation of a rigid body about a fixed axis, depending on both the distribution of mass and the rotational speed.
Definition of Kinetic Energy of a Rotating Body
Rotational kinetic energy refers to the energy possessed by an object due to its rotational motion about a fixed axis. It is distinct from linear kinetic energy and depends on the moment of inertia and the angular velocity of the body.
Expression for Rotational Kinetic Energy
The rotational kinetic energy $K_{rot}$ of a body rotating about a fixed axis is given by:
$K_{rot} = \dfrac{1}{2} I \omega^2$
Here, $I$ represents the moment of inertia, which characterizes the mass distribution about the axis, and $\omega$ denotes the angular velocity. Both parameters determine the magnitude of rotational kinetic energy.
Derivation of the Rotational Kinetic Energy Formula
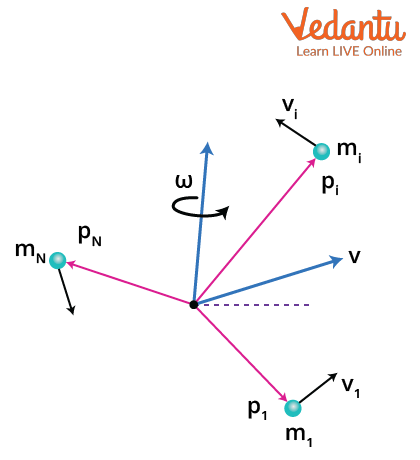
A rigid body can be considered to consist of numerous small particles, each having mass $m_i$ located at a distance $r_i$ from the axis of rotation. The velocity of each particle is $v_i = \omega r_i$ due to the body's rotation.
The kinetic energy of each particle is $\dfrac{1}{2} m_i v_i^2 = \dfrac{1}{2} m_i (\omega r_i)^2$.
Summing over all particles:
$K_{rot} = \sum_{i=1}^{N} \dfrac{1}{2} m_i (\omega r_i)^2 = \dfrac{1}{2} \omega^2 \sum_{i=1}^{N} m_i r_i^2$
The term $\sum_{i=1}^{N} m_i r_i^2$ is the moment of inertia $I$. Thus, $K_{rot} = \dfrac{1}{2} I \omega^2$.
Comparison with Linear Kinetic Energy
For a body undergoing translational motion, kinetic energy is written as $K_{linear} = \dfrac{1}{2} m v^2$. In rotational motion, the moment of inertia $I$ replaces mass $m$ and angular velocity $\omega$ replaces velocity $v$.
This analogy helps connect rotational concepts to linear motion and clarifies the dependence of rotational kinetic energy on both mass distribution and rotational speed.
Dimensional Analysis of the Rotational Kinetic Energy Formula
The dimensions of $K_{rot}$ are derived as follows:
$[K_{rot}] = [I][\omega^2] = [M L^2][T^{-2}] = [M L^2 T^{-2}]$
The SI unit of rotational kinetic energy is the joule (J). This is identical to the unit for kinetic energy in linear motion.
Kinetic Energy of a Rolling Body
For a rigid body rolling without slipping on a surface, its kinetic energy is the sum of translational and rotational components. The total kinetic energy is $K_{total} = \dfrac{1}{2} m v^2 + \dfrac{1}{2} I \omega^2$, where $v$ is the center of mass velocity.
This principle applies to rolling objects such as spheres, cylinders, and rings. More about the moment of inertia can be found in the Moment Of Inertia article.
Solved Example: Calculation of Rotational Kinetic Energy
Consider a solid disk with moment of inertia $I = 500$ kg m$^2$ rotating at angular velocity $\omega = 12$ rad/s. The rotational kinetic energy is:
$K_{rot} = \dfrac{1}{2} \times 500 \times (12)^2 = \dfrac{1}{2} \times 500 \times 144 = 36,000$ J
Such examples illustrate the quantitative application of the formula.
Dependence on Physical Parameters
Rotational kinetic energy of a body is dependent on the moment of inertia, which is determined by the mass distribution with respect to the rotation axis, and on the square of the angular velocity.
Thus, objects with larger motions of inertia or higher angular velocities possess greater rotational kinetic energy. Further analysis can involve angular momentum, addressed in the Angular Momentum Of Rotating Body article.
Dimensional Consistency Using the Principle of Homogeneity
Assume the kinetic energy of a rotating body follows $K = k I^\alpha \omega^\beta$, where $k$ is a dimensionless constant. Using dimensional analysis:
$\left[K\right] = [M L^2 T^{-2}]$
$[I]^\alpha = [M L^2]^\alpha$
$[\omega]^\beta = [T^{-1}]^\beta$
Equating both sides: $[M L^2 T^{-2}] = [M^\alpha L^{2\alpha} T^{-\beta}]$. By comparing powers: $\alpha = 1$, $\beta = 2$.
| Quantity | SI Unit |
|---|---|
| Kinetic Energy (K) | Joule (J) |
| Moment of Inertia (I) | kg m$^2$ |
| Angular Velocity ($\omega$) | rad/s |
Applications and Importance
The concept of rotational kinetic energy is critical in analyzing the motion of rotating systems found in daily life and in examinations. It applies to wheels, machinery, and rolling objects. Understanding this is essential in the study of Work, Energy And Power.
Further study includes the relationship of rotational kinetic energy with other forms, such as energy in simple harmonic motion, which is discussed in the Energy In Simple Harmonic Motion page.
FAQs on Understanding the Kinetic Energy of a Rotating Body
1. What is the kinetic energy of a rotating body?
Kinetic energy of a rotating body is the energy possessed by an object due to its rotational motion about a fixed axis. It is given by:
- K.E. = (1/2) I ω2, where I is the moment of inertia and ω is the angular velocity.
- This formula applies to rigid bodies rotating about a fixed axis.
2. How is kinetic energy of a rotating object derived?
The kinetic energy of a rotating object is derived by summing the kinetic energies of all mass elements in the body:
- Each mass element mi at distance ri from the axis moves with velocity vi = ωri.
- Each has kinetic energy: (1/2) mi vi2 = (1/2) mi ω2 ri2
- Summing for all elements: K.E. = (1/2) ω2 Σ mi ri2 = (1/2) I ω2
3. What is the formula for rotational kinetic energy?
The formula for rotational kinetic energy is:
Kinetic Energy = (1/2) I ω2,
- I = moment of inertia (kg·m2)
- ω = angular velocity (rad/s)
4. What is the difference between kinetic energy of translation and rotation?
Translational and rotational kinetic energies describe different types of motion:
- Translational kinetic energy: Movement in a straight line, K.E. = (1/2) m v2
- Rotational kinetic energy: Spinning about an axis, K.E. = (1/2) I ω2
- Translational: Depends on mass and linear velocity
- Rotational: Depends on moment of inertia and angular velocity
5. What factors affect the kinetic energy of a rotating body?
The kinetic energy of a rotating body depends on:
- Moment of inertia (I): Higher I means higher kinetic energy for the same angular speed.
- Angular velocity (ω): The energy increases with the square of angular velocity.
- Distribution of mass: Mass farther from the axis increases I.
6. Can a body have both rotational and translational kinetic energy?
Yes, a body can have both rotational and translational kinetic energy if it rolls or moves while spinning.
- The total kinetic energy is the sum: (1/2) m v2 + (1/2) I ω2
- Examples: Rolling wheels, spinning planets orbiting stars, moving cylinders.
7. What is moment of inertia, and how does it relate to rotational kinetic energy?
Moment of inertia (I) measures a body's resistance to change in rotational motion. It determines how much rotational kinetic energy a body has at a given speed:
- I depends on the mass and how it's distributed about the axis.
- K.E. increases with both I and ω squared: K.E. = (1/2) I ω2
8. Why is the rotational kinetic energy important in real life?
Understanding rotational kinetic energy helps in designing and analyzing moving machines and natural phenomena:
- It helps in engineering machines like flywheels, turbines, and gears.
- Sports: Spinning tops, wheels, and athletic equipment.
- Planetary science: Rotation of planets and stars.
9. Write the expression for total kinetic energy of a rolling body.
The total kinetic energy of a rolling body (that does not slip) is:
Total K.E. = (1/2) m v2 + (1/2) I ω2
- m = mass of the body
- v = linear velocity of center of mass
- I = moment of inertia about the axis
- ω = angular velocity
10. Explain with an example: How does distribution of mass affect kinetic energy in rotation?
A body with mass farther from the axis has higher moment of inertia and thus higher kinetic energy for the same angular velocity.
- Example: A solid disk and a ring of the same mass and radius. The ring (mass farther out) has greater I and K.E. at the same ω.
- This concept is crucial in physics and engineering designs.
11. Why is the formula for rotational kinetic energy (1/2) I ω2?
The formula (1/2) I ω2 is used because it sums the kinetic energy of all rotating particles:
- Each particle's energy: (1/2) m r2 ω2, summed for total I.
- Moment of inertia (I) generalizes mass for rotation.
- Angular velocity (ω) relates to how fast the body spins.
12. What is rotational kinetic energy class 11?
In Class 11 Physics, rotational kinetic energy refers to the energy due to rotational motion:
- The formula is (1/2) I ω2.
- Covered in the CBSE syllabus under System of Particles and Rotational Motion.
- It helps compare different types of energy for moving bodies.


















