




How Does Effective Gravity Affect Us on Earth and in Space?
Effective gravity is the net acceleration experienced by a body due to the combined influence of true gravitational acceleration and other accelerative effects such as rotation or acceleration of the reference frame. This concept is essential for problems involving non-inertial frames, especially in contexts such as rotating planets or accelerating lifts.
Apparent Forces in Non-Inertial Frames
In a non-inertial or accelerating reference frame, bodies experience additional forces called apparent or pseudo forces. These do not originate from physical interactions but arise due to the acceleration of the observer’s frame. Apparent forces must be included in all calculations within such frames.
For example, in a rotating frame like the Earth's surface, bodies experience a centrifugal force directed away from the axis of rotation. These forces affect observable quantities such as apparent weight, acceleration, and effective gravity. Related principles are further explained in Gravitation Explained.
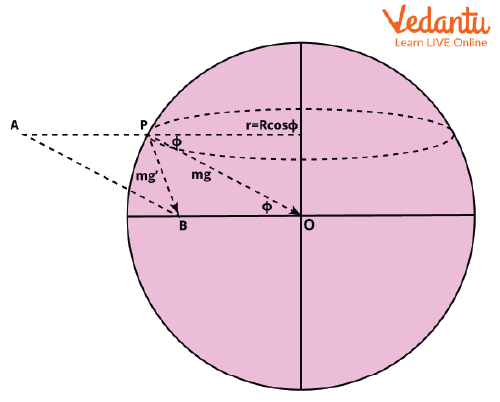
Centrifugal Force due to Rotation
Centrifugal force is an apparent force that acts outward on a mass moving in a circular path, observed from a rotating frame of reference. For an object of mass $m$ at distance $R$ from the axis, with angular velocity $\omega$, the centrifugal force is defined as: $F = -m\omega^2 R$ This force always acts away from the axis of rotation, reducing the net downward force experienced by objects on the Earth's surface.
While centripetal force keeps objects in circular motion towards the center, centrifugal force appears in rotating frames to balance the non-inertial effects, influencing measurements such as weight and acceleration due to gravity on the Earth's surface.
Effective Gravity on the Rotating Earth
On the Earth, the gravitational force acts towards the planet’s center, while the centrifugal force due to Earth’s rotation acts outward and perpendicular to the axis. The effective gravity ($g'$) is the resultant acceleration experienced by a body, given by the vector sum of gravitational and centrifugal accelerations.
The effective gravity does not generally point exactly towards the center of the Earth because the centrifugal acceleration is perpendicular to the axis of rotation. As a result, the value and direction of $g'$ change with latitude.
Mathematical Expression for Effective Gravity
At latitude $\phi$, the effective acceleration due to gravity, considering the centrifugal effect, is: $g' = g - \omega^2 R \cos^2\phi$ where:
- $g$ is the true gravitational acceleration
- $\omega$ is Earth’s angular velocity
- $R$ is Earth’s radius
- $\phi$ is the latitude
At the equator ($\phi=0^\circ$), $\cos^2\phi=1$, so the reduction in effective gravity is maximum. At the poles ($\phi=90^\circ$), $\cos^2\phi=0$, so $g'=g$.
Effective Gravity in Accelerating Reference Frames
When an elevator or lift accelerates, the effective gravity experienced by a body changes. If the lift accelerates upward with acceleration $a$, the effective gravity is $(g+a)$. If it accelerates downward, effective gravity is $(g-a)$. This concept is frequently used in problems involving lifts.
The change in effective gravity in elevators is a direct application of the concept of pseudo force, similar to rotating frames. Such scenarios are covered in Work, Energy, and Power.
Effective Gravity in Fluids and Liquids
When a container with liquid is subjected to acceleration or rotation, the free surface of the liquid aligns perpendicular to the effective gravity vector. This modifies the apparent direction of gravity and leads to the tilting of the liquid surface, which is critical in problems involving rotating vessels.
The concept of effective gravity explains phenomena such as the curved water surface in a rotating bucket or the non-horizontal levels in accelerating tanks.
Comparison: True Gravity vs Effective Gravity
| True Gravity ($g$) | Effective Gravity ($g'$) |
|---|---|
| Acts towards center of mass only | Resultant of gravity and pseudo forces |
| Does not depend on rotation or frame | Depends on rotation and acceleration |
| Uniform for idealized conditions | Varies with location and reference frame |
Solved Example: Effective Gravity at the Equator
Given $g=9.8\,\mathrm{m/s^2}$, $\omega=7.29\times10^{-5}\,\mathrm{rad/s}$, $R=6.37\times10^6\,\mathrm{m}$, and latitude $\phi=0^\circ$ (equator), the reduction in $g$ due to rotation is: $\omega^2R\cos^2\phi = (7.29\times10^{-5})^2 \times 6.37\times10^6\times(1)$ This yields a reduction of approximately $0.034\,\mathrm{m/s^2}$. Therefore, $g' = 9.8 - 0.034 = 9.766\,\mathrm{m/s^2}$
This calculation demonstrates how effective gravity changes with geographical location, which is important for JEE Main and Advanced-level questions. Practice further using the Gravitation Practice Paper.
Key Points on Effective Gravity
- Effective gravity results from vector addition of all accelerative effects
- Earth's rotation reduces effective gravity except at the poles
- In non-inertial frames, pseudo forces must be included
- Effective gravity influences liquid surfaces and apparent weights
Further Study and Practice Resources
For deeper understanding and further practice on effective gravity and related topics, refer to Acceleration Due to Gravity and comprehensive Gravitation Important Questions collections for JEE preparation.
FAQs on Understanding Effective Gravity: Definition, Formula, and Applications
1. What is effective gravity?
Effective gravity is the net acceleration experienced by an object due to the combined effects of earth's gravitational pull and any additional accelerations, such as those caused by earth's rotation.
- It determines how heavy objects feel on Earth's surface.
- It is calculated by combining gravitational acceleration (g) and rotational acceleration.
- At the equator, effective gravity is slightly less than at the poles due to Earth's rotation.
2. How does rotation of the Earth affect effective gravity?
The rotation of the Earth reduces the effective gravity at the equator due to centrifugal force.
- At the equator, centrifugal force acts outward, opposing gravity.
- This force is zero at the poles.
- As a result, objects weigh less at the equator than at the poles.
3. What are the factors affecting effective gravity on the Earth's surface?
Effective gravity depends on multiple factors including
- Latitude: Due to the earth's rotation, centrifugal force is maximum at the equator.
- Altitude: Gravity decreases with increased height above sea level.
- Earth's shape: Oblateness causes gravity to be stronger at the poles.
4. Why is effective gravity less at the equator than at the poles?
Effective gravity is less at the equator because the centrifugal force due to Earth's rotation acts outward, reducing the net gravitational pull.
- The centrifugal force is highest at the equator, lowering effective gravity.
- At the poles, centrifugal force is absent, so gravity is strongest.
- This causes object weights to be slightly less at the equator compared to the poles.
5. How is effective gravity calculated at a latitude θ?
Effective gravity at latitude θ can be calculated using the formula:
- geff = g - Rω2cos2θ
- g = gravitational acceleration
- R = radius of Earth
- ω = angular velocity of Earth
- θ = latitude
6. What is the difference between gravity and effective gravity?
Gravity is the force of attraction between Earth and an object, while effective gravity is the net force experienced after accounting for Earth's rotation.
- Gravity acts towards Earth's center.
- Effective gravity = gravitational force minus centrifugal force due to rotation.
7. Why do objects weigh less at high altitudes?
Objects weigh less at higher altitudes because the distance from Earth's center increases, reducing gravitational pull.
- The gravitational force decreases with the square of the distance from Earth's center.
- This leads to a reduction in effective gravity and, thus, weight.
8. How does effective gravity affect satellites and astronauts?
Effective gravity is much lower for satellites and astronauts in orbit because they experience microgravity due to their continuous free fall around Earth.
- They are in a state of apparent weightlessness.
- Only small tidal forces or minor variations in gravity are experienced.
9. What is the significance of effective gravity in daily life?
Effective gravity determines the weight of objects we measure, influences engineering structures, and affects sports and navigation.
- It is considered in construction, travel, and fitness measurements as object weights can vary slightly by location.
- Pilots and athletes may adjust for slight differences in weight and acceleration.
10. What is the value of effective gravity at the poles and the equator?
The average value of effective gravity is:
- At the poles: approximately 9.83 m/s².
- At the equator: approximately 9.78 m/s².
11. How does Earth's oblateness influence effective gravity?
The Earth's oblateness (flattened at the poles) means the radius is shorter at the poles and longer at the equator, causing gravity to be stronger at the poles than at the equator.
- This change in shape and radius leads to measurable variations in effective gravity worldwide.

































