
What is the period of small oscillations of the block of mass m, if the springs are ideal and pulleys are massless?
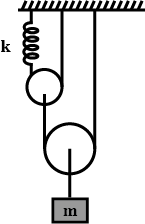
A) $\dfrac{{{\pi }}}{{{2}}}\sqrt {\dfrac{{{m}}}{{{k}}}} $
B) $\dfrac{{{\pi }}}{{{2}}}\sqrt {\dfrac{{{m}}}{{{{2k}}}}} $
C) $\dfrac{{{\pi }}}{{{2}}}\sqrt {\dfrac{{{{2m}}}}{{{k}}}} $
D) ${{\pi }}\sqrt {\dfrac{{{m}}}{{{k}}}} $
Answer
218.1k+ views
Hint: First find the spring constant and then by using the equation that gives the time period of oscillation of a spring in relation to mass of the body and the spring constant find the weight of the body. Here first we will draw the free body diagram of the given system as shown below. And then after balancing the force as discussed below.
Complete step by step solution:
Free body diagram of given pulley-block system as shown in below figure.
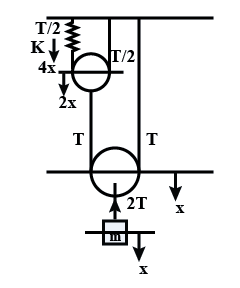
$ \Rightarrow $ $2T$ = $mg$
By using Hooke's law for a spring balance.
$ \Rightarrow $ $mg$ =${{4k}}{{{x}}_{{0}}}$ ………….. (1)
$ \Rightarrow $ $\dfrac{{{T}}}{{{2}}} = {{k}}{{{x}}_{{0}}}$
$ \Rightarrow $ ${{T = 2k}}{{{x}}_{{0}}}$
If displaced
$ \Rightarrow$ $mg−2T$ = $ma$
$ \Rightarrow $ $mg−4k({x_0} + x)$ = $ma$
$ \Rightarrow $ $\dfrac{{{T}}}{{{2}}}$= $k({x_0}+x)$
$ \Rightarrow $ $T$ = $2k({x_0}+x)$
Now,
From equation (1), we will get
$ \Rightarrow $ $mg$ =${{4k}}{{{x}}_{{0}}}$
$ \Rightarrow $ ${{{x}}_{{0}}}{{ = }}\dfrac{{{{mg}}}}{{{{4k}}}}$
As we know,
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{g}}}{{{{{x}}_{{0}}}}}} $
Put ${{{x}}_{{0}}}{{ = }}\dfrac{{{{mg}}}}{{{{4k}}}}$and get
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{g}}}{{\dfrac{{{{mg}}}}{{{{4k}}}}}}} $
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{{4k}}}}{{{m}}}} $
Now, by using the formula of time period as ${{T = }}\dfrac{{{{2\pi }}}}{{{\omega }}}$
Put the value of ${{\omega = }}\sqrt {\dfrac{{{{4k}}}}{{{m}}}} $and we will get
$ \Rightarrow $${{T = 2\pi }}\sqrt {\dfrac{{{m}}}{{{{4k}}}}} $
$ \therefore $${{T = \pi }}\sqrt {\dfrac{{{m}}}{{{k}}}} $
Thus, ${{T = \pi }}\sqrt {\dfrac{{{m}}}{{{k}}}} $ is the period of small oscillations of the block of mass m.
Therefore, option (D) is the correct option.
Note: Mathematically, Hooke's law for a spring balance can be written down as:
F= -kx
Where F is the restoring force,
k is the spring constant of the spring balance and
x is the displacement from the initial position of the spring balance system.
This formula is extremely useful in other chapters also like Simple Harmonic Chapter, Newton's Laws of Motion, etc.
Complete step by step solution:

Free body diagram of given pulley-block system as shown in below figure.

$ \Rightarrow $ $2T$ = $mg$
By using Hooke's law for a spring balance.
$ \Rightarrow $ $mg$ =${{4k}}{{{x}}_{{0}}}$ ………….. (1)
$ \Rightarrow $ $\dfrac{{{T}}}{{{2}}} = {{k}}{{{x}}_{{0}}}$
$ \Rightarrow $ ${{T = 2k}}{{{x}}_{{0}}}$
If displaced
$ \Rightarrow$ $mg−2T$ = $ma$
$ \Rightarrow $ $mg−4k({x_0} + x)$ = $ma$
$ \Rightarrow $ $\dfrac{{{T}}}{{{2}}}$= $k({x_0}+x)$
$ \Rightarrow $ $T$ = $2k({x_0}+x)$
Now,
From equation (1), we will get
$ \Rightarrow $ $mg$ =${{4k}}{{{x}}_{{0}}}$
$ \Rightarrow $ ${{{x}}_{{0}}}{{ = }}\dfrac{{{{mg}}}}{{{{4k}}}}$
As we know,
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{g}}}{{{{{x}}_{{0}}}}}} $
Put ${{{x}}_{{0}}}{{ = }}\dfrac{{{{mg}}}}{{{{4k}}}}$and get
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{g}}}{{\dfrac{{{{mg}}}}{{{{4k}}}}}}} $
$ \Rightarrow $${{\omega = }}\sqrt {\dfrac{{{{4k}}}}{{{m}}}} $
Now, by using the formula of time period as ${{T = }}\dfrac{{{{2\pi }}}}{{{\omega }}}$
Put the value of ${{\omega = }}\sqrt {\dfrac{{{{4k}}}}{{{m}}}} $and we will get
$ \Rightarrow $${{T = 2\pi }}\sqrt {\dfrac{{{m}}}{{{{4k}}}}} $
$ \therefore $${{T = \pi }}\sqrt {\dfrac{{{m}}}{{{k}}}} $
Thus, ${{T = \pi }}\sqrt {\dfrac{{{m}}}{{{k}}}} $ is the period of small oscillations of the block of mass m.
Therefore, option (D) is the correct option.
Note: Mathematically, Hooke's law for a spring balance can be written down as:
F= -kx
Where F is the restoring force,
k is the spring constant of the spring balance and
x is the displacement from the initial position of the spring balance system.
This formula is extremely useful in other chapters also like Simple Harmonic Chapter, Newton's Laws of Motion, etc.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Algebra Made Easy: Step-by-Step Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

How to Convert a Galvanometer into an Ammeter or Voltmeter




