Question

One end of a light spring of force constant \[k\] is fixed to a block A of mass \[M\] placed on a horizontal frictional table, the other end of the spring is fixed to a wall. A smaller block B of a mass \[m\] is placed on a block A. the system is displaced by a small amount and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block? The coefficient of static friction is between the two blocks is

(A) \[\dfrac{{\mu Mg}}{k}\]
(B) \[\dfrac{{\mu mg}}{k}\]
(C) \[\dfrac{{\mu \left( {M + m} \right)g}}{k}\]
(D) None of the above

Answer 1

Hint: For smaller blocks not to fall off, the maximum force on the lower block must be equal to the frictional force between the small block and large block. The force acting on the lower block is provided by the spring attached to it.
Formula used: In this solution we will be using the following formulae;
\[F = ke\] where \[F\] is the elastic force exerted by a string, \[k\] is the string constant and \[e\] is the extension of the string from equilibrium.
\[f = \mu mg\] where \[f\] is the frictional force acting on a surface, \[\mu \] is the coefficient of friction between the surface of the two bodies.

Complete Step-by-Step solution:
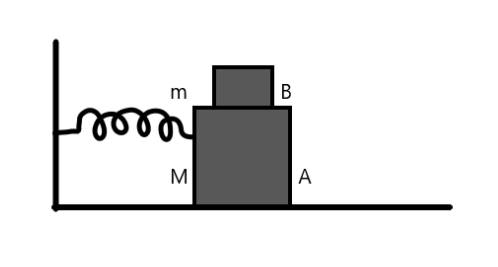
As it is seen, if the lower block is displaced, the spring will exert a restoring force proportional to the extension of the string.
For the block on top not to fall, the maximum force exerted would need to be equal to the maximum static friction between the surfaces of the two blocks.
The force due to a string is given by
\[F = ke\] where \[k\] is the string constant and \[e\] is the extension of the string from equilibrium.
While the frictional force can be given as
\[f = \mu mg\] where \[\mu \] is the coefficient of friction between the surface of the two bodies.
Hence, equating the two, we have that
\[ke = \mu mg\]
Maximum force occurs at amplitude, hence
\[kA = \mu mg\]
\[ \Rightarrow A = \dfrac{{\mu mg}}{k}\]

Hence, the correct option is

Note: For clarity, the reason why the maximum force applied to the lower block must be equal to the surface is due to Newton’s law. When a force is applied to the bottom, the top block, on its own reference frame can be likened to the same amount of force pushing it away from t
the bottom block. If it were moving at a constant velocity, the top block would not fall off, ever.