Question

Let the centroid of an equilateral triangle $ABC$ be at the origin. Let one of the sides of the equilateral triangle be along the straight line $x + y = 3$. If $R$ and $r$ be the radius of the circumcircle and the incircle respectively of a triangle $ABC$. Then what is the value of $R + r$?
A. $2\sqrt 2 $
B. $3\sqrt 2 $
C. $7\sqrt 2 $
D. $\dfrac{9}{{\sqrt 2 }}$

Answer 1

Hint: First, use the formula of the perpendicular distance between a point and a line to find the length of the radius of the incircle. Then use the relation between the radius of the circumcircle and the incircle of an equilateral triangle, and find the radius of the circumcircle. In the end, add the values of the radius of the circumcircle and the incircle of an equilateral triangle to get the required answer.

Formula Used:
The perpendicular distance between a point $\left( {p,q} \right)$ and a line $ax + by + c = 0$ is:
$d = \left| {\dfrac{{ap + bq + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$
The relation between the radius of the circumcircle and the incircle of an equilateral triangle is: $R = 2r$

Complete step by step solution:
Given: The origin is a centroid of an equilateral triangle $ABC$.
One of the sides of the equilateral triangle is along the straight line $x + y = 3$.
$R$ and $r$ be the radius of the circumcircle and the incircle respectively.


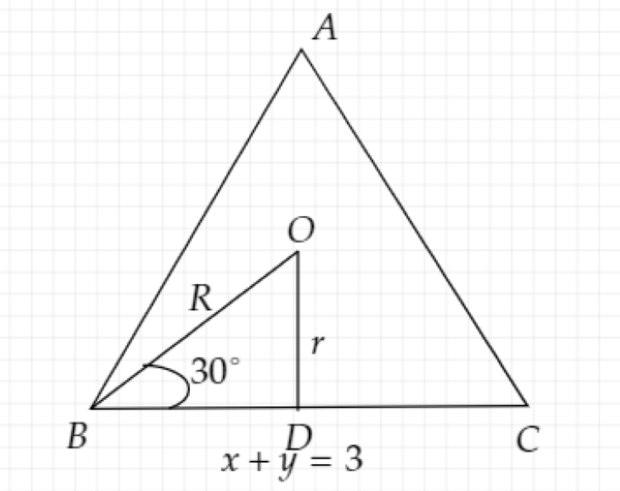
Image: An equilateral triangle ABC with a centroid (0, 0)

The perpendicular distance between the origin and a line $x + y = 3$ is the radius of incircle.
Now apply the formula of the perpendicular distance between a point and a line.
The length of radius of the incircle is,
$r = \left| {\dfrac{{0\left( 1 \right) + 0\left( 1 \right) - 3}}{{\sqrt {{1^2} + {1^2}} }}} \right|$
$ \Rightarrow r = \left| {\dfrac{{ - 3}}{{\sqrt 2 }}} \right|$
$ \Rightarrow r = \dfrac{3}{{\sqrt 2 }}$
We know that in an equilateral triangle, the length of the radius of the circumcircle is twice the length of the radius of the incircle.
So, $R = 2r$.
Substitute $r = \dfrac{3}{{\sqrt 2 }}$ in the above equation.
$R = 2\left( {\dfrac{3}{{\sqrt 2 }}} \right)$
$ \Rightarrow R = \dfrac{6}{{\sqrt 2 }}$
Therefore,
$R + r = \dfrac{6}{{\sqrt 2 }} + \dfrac{3}{{\sqrt 2 }}$
$ \Rightarrow R + r = \dfrac{9}{{\sqrt 2 }}$

Option ‘D’ is correct

Note: The distance between the orthocenter of a triangle and the side of the triangle is the radius of the incircle of the triangle. For an equilateral triangle, the radius of the circumcircle is the same as the diameter of the incircle of the triangle.