
Let $\overrightarrow{\mathrm{P}}$ be the linear momentum of a particle whose position vector is $\overrightarrow{\mathrm{r}}$ with respect to the origin and $\overrightarrow{\mathrm{L}}$ be the angular momentum at this particle about the origin then:
(A) 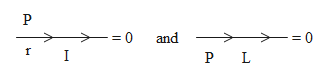
(B) 
(C) 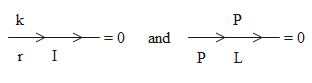
(D) 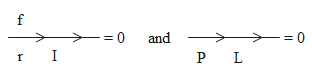
Answer
214.8k+ views
Hint: We know that momentum is a physics term that refers to the quantity of motion that an object has. A sports team that is on the move has momentum. If an object is in motion (on the move) then it has momentum. One example is the use of airbags in automobiles. Airbags are used in automobiles because they are able to minimize the effect of the force on an object involved in a collision. Airbags accomplish this by extending the time required to stop the momentum of the driver and passenger. Momentum is mass in motion, and any moving object can have momentum. An object's change in momentum is equal to its impulse. Impulse is a quantity of force times the time interval. Impulse is not equal to momentum itself; rather, it's the increase or decrease of an object's momentum. Based on this concept we have to solve this question
Complete step by step answer
We know that,
$\overrightarrow{\mathrm{P}}$
Hence, we can determine that,
$\left| \overrightarrow{\text{L}}\times \overrightarrow{\text{P}} \right|=0$
Accordingly, we can say that,
$\left| \overrightarrow{\text{r}}\times \overrightarrow{\text{I}} \right|=0$
Since, I is the moment of Inertia
Therefore, the correct answer is Option B.
Note: We should know that linear momentum is defined as the product of a system's mass multiplied by its velocity. In symbols, linear momentum is expressed as $p=mv$. Momentum is directly proportional to the object's mass and also its velocity. Thus, the greater an object's mass or the greater its velocity, the greater its momentum. Note that the linear moment is a vector quantity and is conserved in any direction. In the center-of-mass system, the total momentum is always zero, before and after the interaction, in any direction. Angular momentum is inertia of rotation motion. Linear momentum is inertia of translation motion. The big difference is that the type of motion which is related to each momentum is different. It is important to consider the place where the force related to rotation applies, which is appears as 'r' in the formula
Complete step by step answer
We know that,
$\overrightarrow{\mathrm{P}}$
Hence, we can determine that,
$\left| \overrightarrow{\text{L}}\times \overrightarrow{\text{P}} \right|=0$
Accordingly, we can say that,
$\left| \overrightarrow{\text{r}}\times \overrightarrow{\text{I}} \right|=0$
Since, I is the moment of Inertia
Therefore, the correct answer is Option B.
Note: We should know that linear momentum is defined as the product of a system's mass multiplied by its velocity. In symbols, linear momentum is expressed as $p=mv$. Momentum is directly proportional to the object's mass and also its velocity. Thus, the greater an object's mass or the greater its velocity, the greater its momentum. Note that the linear moment is a vector quantity and is conserved in any direction. In the center-of-mass system, the total momentum is always zero, before and after the interaction, in any direction. Angular momentum is inertia of rotation motion. Linear momentum is inertia of translation motion. The big difference is that the type of motion which is related to each momentum is different. It is important to consider the place where the force related to rotation applies, which is appears as 'r' in the formula
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction, Transfer of Energy Important Concepts and Tips for JEE

JEE Analytical Method of Vector Addition Important Concepts and Tips

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Equation of Trajectory in Projectile Motion: Derivation & Proof

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Hybridisation in Chemistry – Concept, Types & Applications

Angle of Deviation in a Prism – Formula, Diagram & Applications

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Collision: Meaning, Types & Examples in Physics




