
Infinite current-carrying conductor \[PQ\] . $AB$ and $CD$ are smooth conducting rods on which a conductor $EF$ moves with constant velocity $V$ as shown in the figure. The force needed to maintain a constant speed $EF$ is
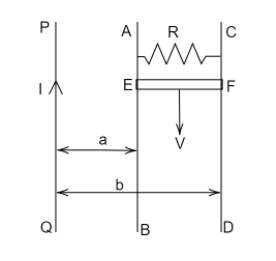
Answer
219.3k+ views
Hint: Find the magnetic field due to the current-carrying wire. Use this magnetic field equation to find the induced emf between $EF$ . Using Ohm’s law, find the current in the loop and hence find the force required to maintain the constant speed.
Complete Step by step solution:
The equation for the magnetic field around the current-carrying wire at a distance $r$ is given by
$\Rightarrow$ $B=\dfrac{{{\mu }_{o}}I}{2\pi r}$
Emf induced by the current-carrying rod $PQ$ on the rod $EF$ is given by
$\Rightarrow$ $emf=\int\limits_{a}^{b}{BVdr}$
Substituting the already written equation for the magnetic field into the above equation, we get
$\Rightarrow$ $emf=\int\limits_{a}^{b}{\dfrac{{{\mu }_{o}}I}{2\pi r}Vdr}$
After integration and substituting the lower and upper limit into the integrated term, we get
$\Rightarrow$ $emf=\dfrac{{{\mu }_{o}}IV}{2\pi }\ln \left( \dfrac{b}{a} \right)$
By Ohm's law,
$I=\dfrac{V}{R}$
Therefore, using OHM’s law, we get the current due to induced emf as
$i=\dfrac{emf}{R}$
By substituting the derived equation for emf in the above equation for current, we get
$\Rightarrow$ $i=\dfrac{{{\mu }_{o}}IV}{2\pi R}\ln \left( \dfrac{b}{a} \right)$
Now, the force on the induced current-carrying rod due to the magnetic field produced due to the current flowing through the rod $PQ$ is given by
$\Rightarrow$ $F=\int\limits_{a}^{b}{Bidr}$
By substituting the equations for the magnetic field and the induced current, we get
$F=\int\limits_{a}^{b}{\dfrac{{{\mu }_{o}}I}{2\pi r}\dfrac{{{\mu }_{o}}IV}{2\pi R}\ln \left( \dfrac{b}{a} \right)dr}$
Integrating the above equation and substituting the upper and lower limits to the integrated equation gives us
$\Rightarrow$ $F=\dfrac{V}{R}{{\left( \dfrac{{{\mu }_{o}}I}{2\pi }\ln \left( \dfrac{b}{a} \right) \right)}^{2}}$
This is the force required to move the rod $EF$ at a constant velocity $V$ .
Note:
Force on a current-carrying conductor is given by
$F=BIL\sin \theta $
Here, $\theta $ is the angle subtended between the conductor and the direction of the magnetic field. In the given question, the angle between the conductor and the magnetic field is found to be ${{90}^{\circ }}$ . So, $\sin \theta $ becomes $1$ and that is the reason we don’t see the sine term in the equation.
Complete Step by step solution:
The equation for the magnetic field around the current-carrying wire at a distance $r$ is given by
$\Rightarrow$ $B=\dfrac{{{\mu }_{o}}I}{2\pi r}$
Emf induced by the current-carrying rod $PQ$ on the rod $EF$ is given by
$\Rightarrow$ $emf=\int\limits_{a}^{b}{BVdr}$
Substituting the already written equation for the magnetic field into the above equation, we get
$\Rightarrow$ $emf=\int\limits_{a}^{b}{\dfrac{{{\mu }_{o}}I}{2\pi r}Vdr}$
After integration and substituting the lower and upper limit into the integrated term, we get
$\Rightarrow$ $emf=\dfrac{{{\mu }_{o}}IV}{2\pi }\ln \left( \dfrac{b}{a} \right)$
By Ohm's law,
$I=\dfrac{V}{R}$
Therefore, using OHM’s law, we get the current due to induced emf as
$i=\dfrac{emf}{R}$
By substituting the derived equation for emf in the above equation for current, we get
$\Rightarrow$ $i=\dfrac{{{\mu }_{o}}IV}{2\pi R}\ln \left( \dfrac{b}{a} \right)$
Now, the force on the induced current-carrying rod due to the magnetic field produced due to the current flowing through the rod $PQ$ is given by
$\Rightarrow$ $F=\int\limits_{a}^{b}{Bidr}$
By substituting the equations for the magnetic field and the induced current, we get
$F=\int\limits_{a}^{b}{\dfrac{{{\mu }_{o}}I}{2\pi r}\dfrac{{{\mu }_{o}}IV}{2\pi R}\ln \left( \dfrac{b}{a} \right)dr}$
Integrating the above equation and substituting the upper and lower limits to the integrated equation gives us
$\Rightarrow$ $F=\dfrac{V}{R}{{\left( \dfrac{{{\mu }_{o}}I}{2\pi }\ln \left( \dfrac{b}{a} \right) \right)}^{2}}$
This is the force required to move the rod $EF$ at a constant velocity $V$ .
Note:
Force on a current-carrying conductor is given by
$F=BIL\sin \theta $
Here, $\theta $ is the angle subtended between the conductor and the direction of the magnetic field. In the given question, the angle between the conductor and the magnetic field is found to be ${{90}^{\circ }}$ . So, $\sin \theta $ becomes $1$ and that is the reason we don’t see the sine term in the equation.
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction Explained: Definition, Examples & Science for Students

Analytical Method of Vector Addition Explained Simply

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses




