
In triangle ABC, right-angled at B, if $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$, find the value of:
i) $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$
ii) $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$
Answer
241.2k+ views
Hint: Use the right-angle triangle Pythagoras theorem. Find the values of $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ and $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$. Right angle means the angle is $90^\circ $. It consists of six trigonometric ratios such as $sin, cos, tan, cot, sec$ and $cosec$.
Complete step by step solution:
We know from the problem that $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$.
With the help of above information we can draw the right-angle triangle as we know that tan A is the ratio of perpendicular and base of a right angled triangle.
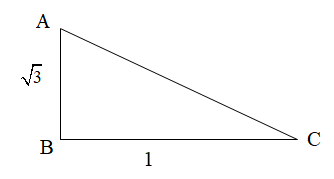
Now, apply the right-angle triangle Pythagoras theorem for the above triangle.
${\left( {{\rm{Hypotenuse}}} \right)^2} = {\left( {{\rm{Height}}} \right)^2} + {\left( {{\rm{Base}}} \right)^2}\\
{\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$
Substitute the values from the above diagram \[{\rm{AB}} = \sqrt 3\] and \[{\rm{BC}} = 1\] in ${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$.
${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}\\
= {\left( {\sqrt 3 } \right)^2} + {\left( 1 \right)^2}\\
= 3 + 1\\
= 4$
We can take the square root of the above equation.
${\rm{AC}} = \sqrt 4 \\
= 2$
Hence, the hypotenuse of the triangle from the above result is 2.
Now we also calculate the value of $\sin {\rm{A}}$ from the formula below.
$\sin {\rm{A}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\sin {\rm{A}}$ from the above result is $\dfrac{1}{2}$.
Now, we also calculate the value of $\cos {\rm{A}}$ from the formula below.
$\cos {\rm{A}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\cos {\rm{A}}$ from the above result is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\sin {\rm{C}}$:
$\sin {\rm{C}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\sin {\rm{C}}$ is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\cos {\rm{C}}$:
$\cos {\rm{C}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\cos {\rm{C}}$ is $\dfrac{1}{2}$.
(i) Solve the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
$\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{1}{2}} \right)\left( {\dfrac{1}{2}} \right) + \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{1}{4} + \dfrac{3}{4}\\
= \dfrac{4}{4}\\
= 1$
Hence, the value of the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ is 1.
(ii) Solve the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
$cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{1}{2}} \right) - \left( {\dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{{\sqrt 3 }}{4} - \dfrac{{\sqrt 3 }}{4}\\
= 0
$
Hence, the value of the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$ is 0.
Note: Here we use the Pythagoras theorem to solve the trigonometric values such as $\sin {\rm{A }}$ and $\cos{\rm{A}}$. The trigonometric values cosec, sec and cot are the opposite values of sin, cos and tan respectively.
Complete step by step solution:
We know from the problem that $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$.
With the help of above information we can draw the right-angle triangle as we know that tan A is the ratio of perpendicular and base of a right angled triangle.
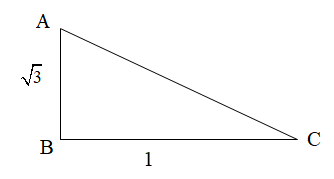
Now, apply the right-angle triangle Pythagoras theorem for the above triangle.
${\left( {{\rm{Hypotenuse}}} \right)^2} = {\left( {{\rm{Height}}} \right)^2} + {\left( {{\rm{Base}}} \right)^2}\\
{\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$
Substitute the values from the above diagram \[{\rm{AB}} = \sqrt 3\] and \[{\rm{BC}} = 1\] in ${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$.
${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}\\
= {\left( {\sqrt 3 } \right)^2} + {\left( 1 \right)^2}\\
= 3 + 1\\
= 4$
We can take the square root of the above equation.
${\rm{AC}} = \sqrt 4 \\
= 2$
Hence, the hypotenuse of the triangle from the above result is 2.
Now we also calculate the value of $\sin {\rm{A}}$ from the formula below.
$\sin {\rm{A}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\sin {\rm{A}}$ from the above result is $\dfrac{1}{2}$.
Now, we also calculate the value of $\cos {\rm{A}}$ from the formula below.
$\cos {\rm{A}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\cos {\rm{A}}$ from the above result is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\sin {\rm{C}}$:
$\sin {\rm{C}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\sin {\rm{C}}$ is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\cos {\rm{C}}$:
$\cos {\rm{C}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\cos {\rm{C}}$ is $\dfrac{1}{2}$.
(i) Solve the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
$\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{1}{2}} \right)\left( {\dfrac{1}{2}} \right) + \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{1}{4} + \dfrac{3}{4}\\
= \dfrac{4}{4}\\
= 1$
Hence, the value of the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ is 1.
(ii) Solve the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
$cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{1}{2}} \right) - \left( {\dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{{\sqrt 3 }}{4} - \dfrac{{\sqrt 3 }}{4}\\
= 0
$
Hence, the value of the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$ is 0.
Note: Here we use the Pythagoras theorem to solve the trigonometric values such as $\sin {\rm{A }}$ and $\cos{\rm{A}}$. The trigonometric values cosec, sec and cot are the opposite values of sin, cos and tan respectively.
Recently Updated Pages
Geometry of Complex Numbers Explained

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Trending doubts
JEE Main 2026: Session 1 Results Out and Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

JEE Main Participating Colleges 2026 - A Complete List of Top Colleges

Clemmensen and Wolff Kishner Reductions Explained for JEE & NEET

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding the Angle of Deviation in a Prism

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

Inductive Effect and Its Role in Acidic Strength

Hybridisation in Chemistry – Concept, Types & Applications

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Understanding the Electric Field of a Uniformly Charged Ring




