Question

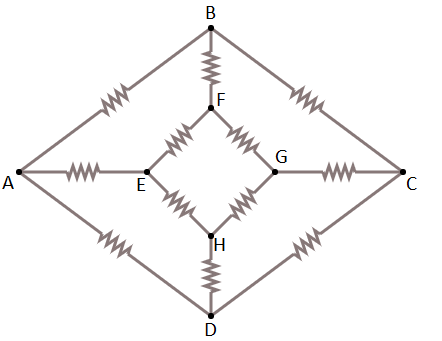
In the network shown in figure each resistance is $R$. The equivalent resistance between $A\& B$ is:

A) $\dfrac{{3R}}{4}$
B) $\dfrac{{5R}}{6}$
C) $\dfrac{{7R}}{{12}}$
D) $\dfrac{{4R}}{{13}}$

Answer 1

Hint: 1. Resistors are said to be connected in parallel if the current flow each resistor is different.
2. If two resistance or impedances are connected in parallel are equal and of the same value. The total or equivalent resistance ${R_T}$ is equal to the half the value of one resistor. That is equal to $\dfrac{R}{2}$ for two resistor in parallel and for three equal resistors connected in parallel is $\dfrac{R}{3}$ and four it is $\dfrac{R}{4}$.
3. Treated current as water in case of solving the resistances problems. If the current or water flows by the same amount then the connection is in series.
If the $\dfrac{{Current}}{{Water}}$ is distributed or divided among the parts then it is in parallel.

Complete step by step solution:
The given figure is

Step 1: Here if we connected the battery between $A{{ \& C}}$ , then there is no current flow between the resistances between $B{{ \& F}}$ and between the $H{{ \& D}}$ . It is because the current is treated as a balanced wheatstone bridge.
So they can be removed and the corresponding equivalent figure here we have is.

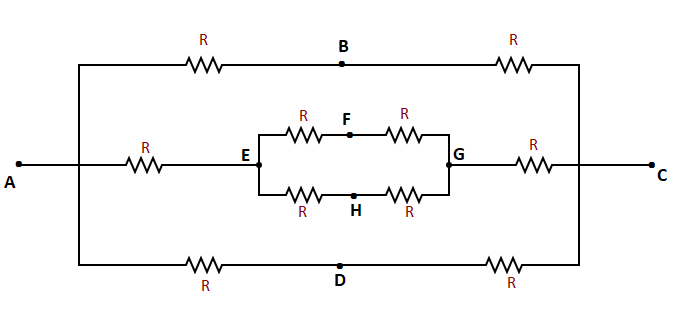
On simplifying the above figure,

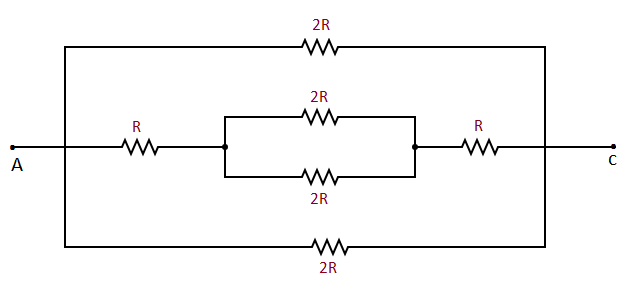
Now further the above figure can be solved as,

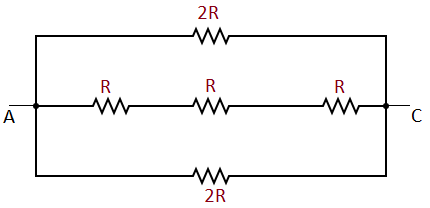
Furthur the above figure can be simplified as shown in the below figure,

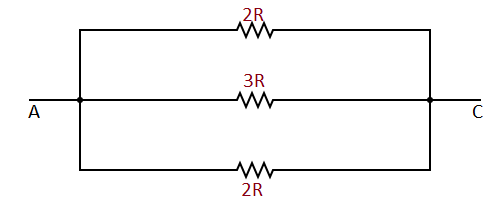
In the above figure all three resistances in parallel.
Now in according the above figure $\left( {1.02} \right)$
The equivalent resistance between $E{{ \& G}}$ is
${R_{EG}} = \dfrac{{\left( {R + R} \right)\left( {R + R} \right)}}{{\left( {R + R} \right) + \left( {R + R} \right)}} = \dfrac{{\left( {2R} \right)\left( {2R} \right)}}{{\left( {2R} \right) + \left( {2R} \right)}}$
Now here we have
${R_{EG}} = \dfrac{{4{R^2}}}{{4R}} = R$
${R_{EG}} = R$
Now net resistance is
${R_{AC}} = \dfrac{{3R}}{4}$

Therefore, option (A) is correct.

Note:
Principle of wheatstone bridge: The wheatstone bridge principle states that if for resistance $P,Q,R\,{{\& S}}$ are arranged to form a bridge with a cell and key between $A$ and $C$ and a galvanometer between $B$ and $D$ the bridge is said to be balanced when the galvanometer shows no deflection.

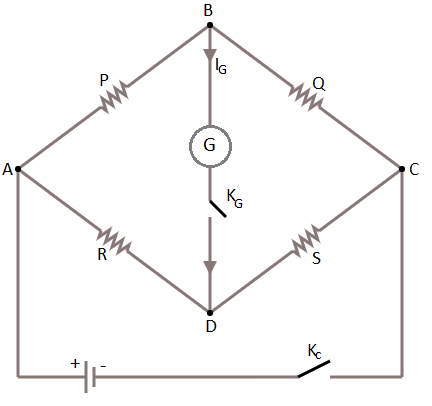
The arrangement of a wheatstone bridge is as shown in the figure $\left( {2.01} \right)$
As if a wheatstone bridge is said to be balanced then
$\dfrac{P}{Q} = \dfrac{R}{S}$
In case when the galvanometer shows no deflection.