Question

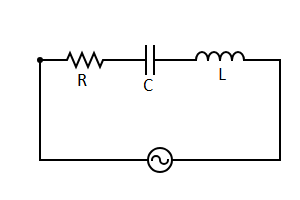
In the given circuit the phase difference between voltage across R and voltage across C is


(A) zero
(B) $\dfrac{\pi }{2}$
(C) $\pi $
(D) $\dfrac{{3\pi }}{2}$

Answer 1

Hint: In an RC ac circuit it is better to draw the phase diagram. It gives a better understanding of phase angles.

Complete step by step solution:
The phase diagram for an ac circuit tells us about the phase angle of current and voltage. It is usually drawn for an RC circuit, RL circuit, LC circuit and RLC circuit. In it we usually find the phase angles of currents flowing through all the elements of the circuit with respect to current through the resistor.
 The circuit given in the question is an RLC circuit.
This circuit will have some reactance along with resistance. Also it will not have an equivalent resistance but an equivalent impedance (Z).
This phase difference $\phi $ depends upon the reactive value of the components being used and hopefully we know that reactance, (X) is zero if the circuit element is resistive, positive if the circuit element is inductive and negative if it is capacitive.
Now let’s say that, for current through R, the instantaneous current will be given by;
$i = {i_0}\sin (\omega t)$ (${i_0}$is the maximum value of the current)
Also, instantaneous voltage will be;
${v_r} = {v_0}\sin (\omega t)$ (${v_0}$ is the maximum value of voltage) ---------eq. (1)
But for capacitor the value of instantaneous charge in the capacitor will be;
$q = {q_0}\sin (\omega t) = C{v_0}\sin (\omega t)$ (${q_0}$ is the maximum charge)
Thus by differentiating the above equation with respect to time we get;
${i_c} = C{v_0}\omega \cos (\omega t)$ (${i_c}$ is the instantaneous current through the capacitor)
Hence instantaneous voltage across capacitor is given by;
${i_c}{X_c} = {v_c} = {v_0}\sin (\omega t + \dfrac{\pi }{2})$ -----eq. (2)
From equation: 1 and equation: 2 we get that the angle between the phase of voltage across resistance and phase of voltage across capacitor is 90 degree.
In an ac RLC circuit the instantaneous current through the resistor and voltage across resistor are in phase. But the voltage across the capacitor lags by 90 degrees. The diagram below shows the angle between voltage across resistor and voltage across capacitor is 90 degree.

Hence option (B) is correct.

Note:
1. Voltage across the inductor leads by 90 degrees from voltage across the resistor.
2. Voltage across resistor and current across resistor are in phase.
3. Angle between the phases of voltage across the inductor and voltage across the capacitor is 180 degrees.