Question

In the given circuit diagram, calculate the current through each resistor.

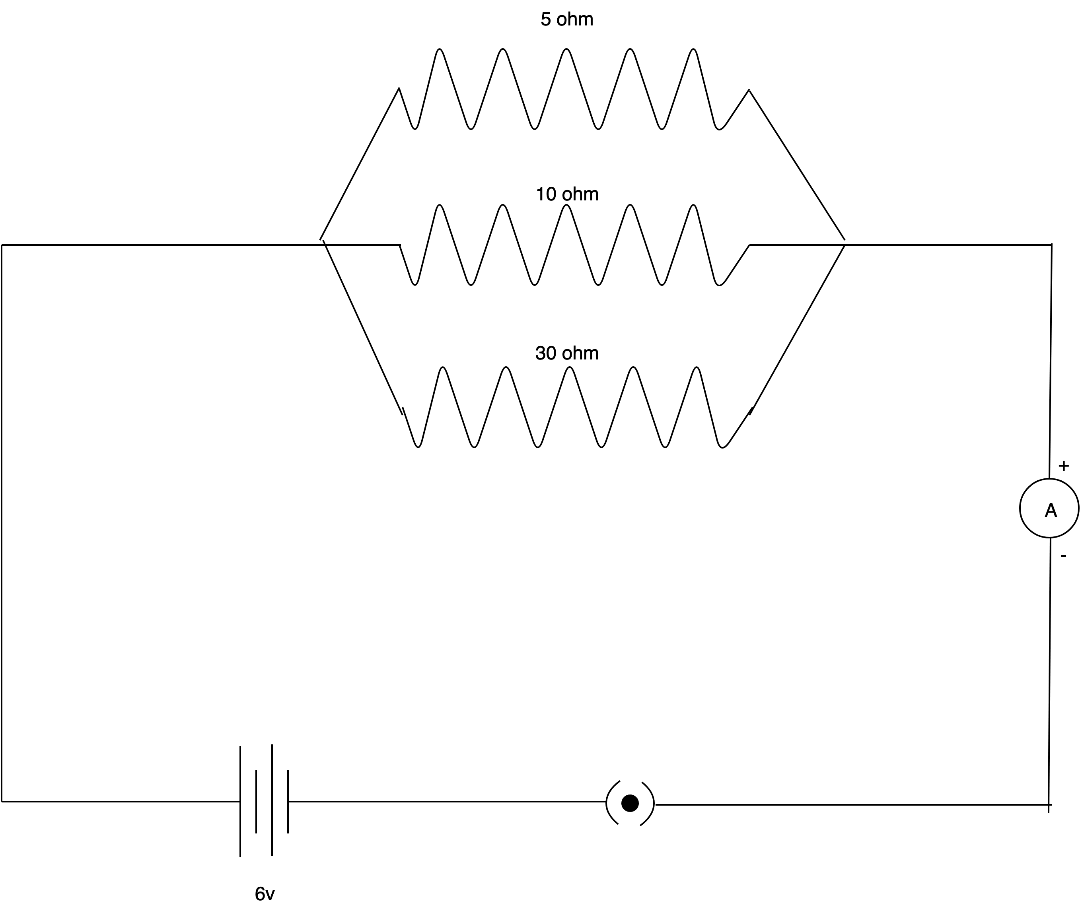
Answer 1

Hint: In the above diagram three resistors are connected in a parallel manner. And the same current is entering each resistor. The total current entering in a parallel resistor circuit is the sum of all individual currents flowing in all the parallel branches. But the amount flowing through each parallel branch may not necessarily be the same, as the resistive value of each branch determines the amount of current flowing through the branch.

Complete step by step solution: Kirchhoff’s current law state that the total current leaving a circuit is equal to that entering the circuit. Which means that no current is lost. Therefore the total current entering the circuit will be equal to the sum of the amount of the current through each resistor. Then by using Ohm’s law the current flowing through each resistor can be calculated.
Step 1: Ohm’s law states that the voltage across the conductor is directly proportional to the current flowing through it, provided all physical conditions remain the same. Now express the relation of voltage, resistor, and the current flowing through the circuit.
First, let us calculate the current through the 5-ohm resistor.
$\therefore {I_5} = \dfrac{V}{{{R_5}}}$ , where ${I_5}$ is the current flowing through the resistor ${R_5}$ .
Substitute the values 6 for $V$ and 5 for ${R_5}$ .
$\therefore {I_5} = \dfrac{6}{5}$
$ \Rightarrow {I_5} = 1.2$ amps.
Step 2: Now for the remaining two resistors we can calculate the amount of current is the same as above. Let us calculate for the 10-ohm resistor.
Again express the same formula.
$\therefore {I_{10}} = \dfrac{V}{{{R_{10}}}}$
Substitute the value 10 for ${R_{10}}$ .
$\therefore {I_{10}} = \dfrac{6}{{10}}$
$ \Rightarrow {I_{10}} = 0.6$ amps.
Step 3: express the formula again to calculate the current through the 30-ohm resistor.
$\therefore {I_{30}} = \dfrac{V}{{{R_{30}}}}$
Substitute the values for $V$ and ${R_{30}}$ .
$\therefore {I_{30}} = \dfrac{6}{{30}}$
$ \Rightarrow {I_{30}} = 0.2$ amps.

Hence the amount of current flowing through the 5-ohm is 1.2 amps, through 10-ohm is 0.6 amps and through 30-ohm is 0.2 amps.

Note: while solving questions about resistors you should always find out carefully whether the resistors are connected parallel or in a series. In the above question the total current flowing through the circuit $ = {I_5} + {I_{10}} + {I_{30}} = 1.2 + 0.6 + 0.2 = 2$ amps. We can verify it by Ohm’s law. First, calculate the total resistance in the circuit.
$\therefore \dfrac{1}{{{R_{total}}}} = \dfrac{1}{{{R_5}}} + \dfrac{1}{{{R_{10}}}} + \dfrac{1}{{{R_{30}}}}$
$ \Rightarrow \dfrac{1}{{{R_{total}}}} = \dfrac{1}{5} + \dfrac{1}{{10}} + \dfrac{1}{{30}}$
$ \Rightarrow \dfrac{1}{{{R_{total}}}} = \dfrac{{10}}{{30}}$
$ \Rightarrow {R_{total}} = \dfrac{{30}}{{10}} = 3$ ohm.
Now express Ohm’s formula.
$V = {I_{total}} \times {R_{total}}$
Now substitute the values 2 for ${I_{total}}$ and 3 for ${R_{total}}$ .
$V = 2 \times 3 = 6$ volt.
Which is exactly the voltage we have in our circuit.
Hence our answer is correct.