Question

In the following diagram, the reading of an ideal voltmeter in the circuit is:
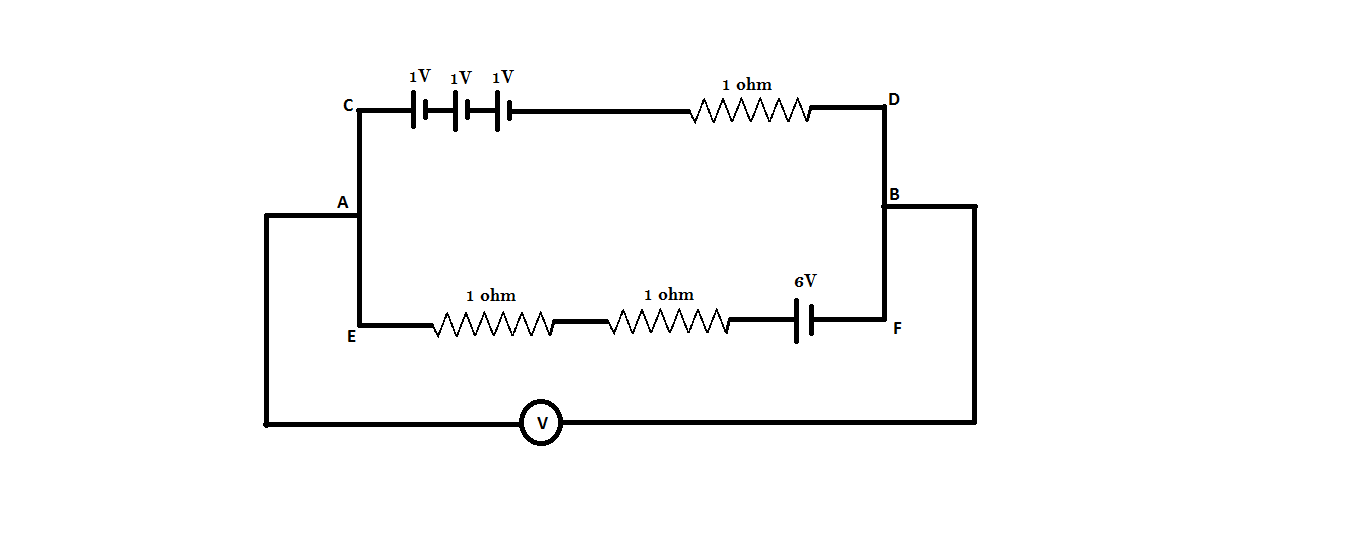A) Zero
B) 2V
C) 4V
D) 6V

Answer 1

Hint: A voltmeter is an instrument used for measuring the electric potential difference between two points in an electric circuit. In the above question, we have to find the potential difference between two points A and B. Use Kirchhoff’s second law of the circuit. Kirchhoff's second law states that the voltage around a loop equals the sum of every voltage drop in the same loop for any closed network and also equals zero. Another thing to keep in mind is that the voltmeter which is connected to the circuit is ideal. An ideal voltmeter is a voltmeter that has infinite resistance, that is, the voltmeter will not allow any amount of current to go through it.

Complete step by step solution:
Step 1: To simplify the diagram we can add two resistors of 1ohm each. Both resistors are in the series combination. To add the resistors in series use the formula $R = {R_1} + {R_2}$ . then our resistance will be 2 ohms and the diagram will look like following
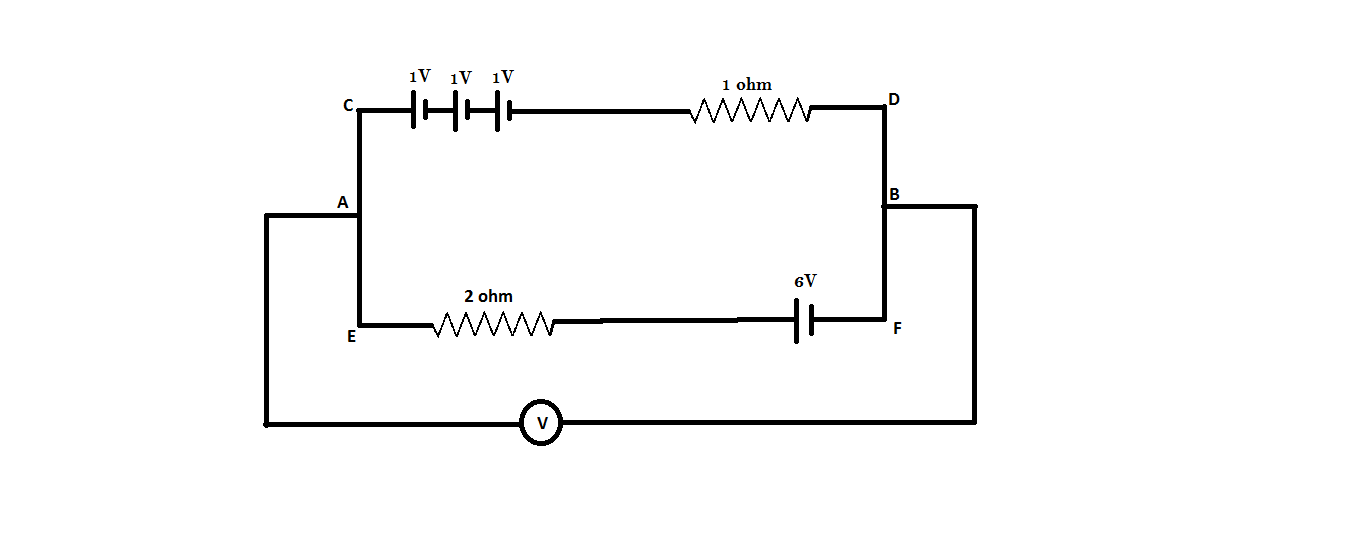Step 2: Three batteries are connected in a series combination therefore we can directly add all the three potential differences and can write as a single potential difference which will be 3V. and we can have the following diagram
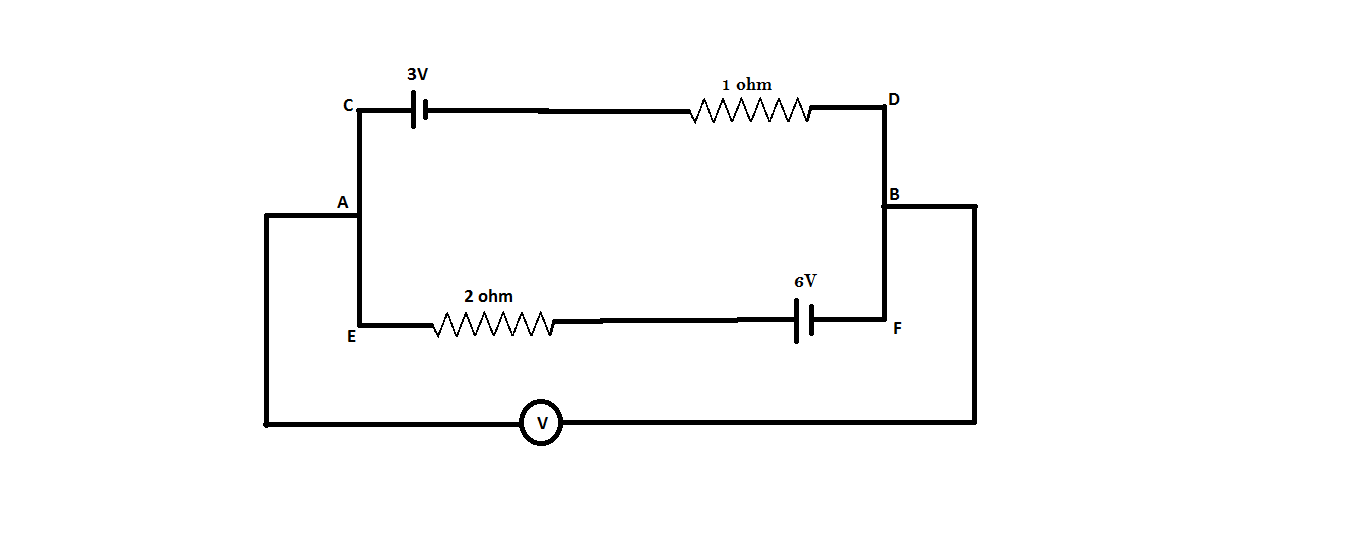Step 3: now apply Kirchhoff’s second law assuming that the current is flowing counterclockwise in the circuit. Let the current flowing in the circuit is $i$ then add all the potential in the circuit and put equal to zero. Since we know the formula, $V = IR$ we can put the potential difference because of each resistor. Therefore,
$\therefore - 6 + 1 \times i - 3 + 2i = 0$
$ \Rightarrow - 9 + 3i = 0$
$ \Rightarrow i = \dfrac{9}{3} = 3$
Therefore the current flowing in the circuit is 3A.
Step 4: now we know the amount of current flowing in the circuit and use this for the calculation of the potential difference between point A and point B. therefore
$\therefore {V_A} - 6 + 2 \times i = {V_B}$ , where ${V_A}$ and ${V_B}$ are the potential at point A and B respectively.
Step 5: For the potential difference we need to calculate the value of the ${V_A} - {V_B}$ . Therefore put the value of $i$ and calculate the desired result
$\therefore {V_A} - {V_B} = 6 - 2 \times 3$
$ \Rightarrow {V_A} - {V_B} = 0$
Therefore the reading in the voltmeter will be zero.

Hence option A is correct.

Note: The sign taken for potential in the above solution depends on the direction of the current flowing in the circuit. If we take the flowing current clockwise then the sign of every potential will be changed. But the result, that is, the amount of current will not change.