Question

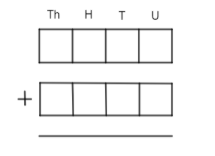
In the figure, two four digit numbers are to be formed by filling the places with digits. The number of different ways in which the places can be filled by the digits so that the sum of the numbers formed is also a four-digit number and in no place there is addition with carrying, is equal to


(a). ${{55}^{6}}$
(b). 220
(c). ${{45}^{4}}$
(d). 219

Answer 1

Hint: In this question, we are given to find the digits so that there will be no carrying over of the digits at any place and that the sum should also be a 4-digit number. Therefore, we can see that for the condition of no carrying over, the sum of the digits can be at most nine in a given column. Also, as the sum of the numbers has to be a four-digit number, the thousands place cannot be equal to zero.

Complete step-step answer:

In this question, we see that if there is no carrying at any of the places, then the sum of the digits in each column can be at most nine. Let us first look at the unit’s column.
Let the digit in the unit’s place of the first number be x, as the sum of the digits of the two numbers can be at most 9, the digit in the unit’s place of the second number can be anything from 0 up to 9-x. However, as x is a digit of the unit’s place in the first number, it can vary from 0 to 9 itself. Therefore, for each value of x, we will get 10-x (the digit can vary from 0 to 9-x which are 10 numbers in total) ways of filling the units place of the second number.

Thus, the number of ways in which the units place of the two numbers can be filled is
$\begin{align}
  & \sum\limits_{x=0}^{x=9}{10-x}=\left( 10-0 \right)+\left( 10-1 \right)+\left( 10-2 \right)+...+\left( 10-9 \right) \\
 & =10\times 10-\left( 0+1+....+9 \right)=100-\dfrac{9\times 10}{2}=55...............(1.1) \\
\end{align}$
Where we have used the fact that the sum of first n natural numbers is equal to $\dfrac{n(n+1)}{2}$.
The filling of the ten’s and the hundred’s places will be exactly similar and we would get 55 ways for each of them as obtained in equation (1.1) …………………………….(1.2)
However, we note that to obtain a four-digit number, the thousands place should not be equal to 0 in the sum. Therefore, the combination of 0 both in the thousand’s place of both numbers has to be discarded. Comparing to equation (1.1), the number of ways of filling the thousand place of the two numbers should be equal to 54…………………………………. (1.3)
Therefore, from equations (1.1), (1.2) and (1.3), we get that the total number of ways of filling the digits is 55+55+55+54=219
Which matches option (d) and thus option(d) is the correct answer to the question.

Note: In obtaining the equation (1.3), we just removed one possibility of the digits being 0 and 0 in the thousand place of both the numbers. However, one can use a similar analysis as used to derive equation (1.1) except that when x is 0, the digit of the other number can vary from 1 to 9 and not 0 to 9.