Question

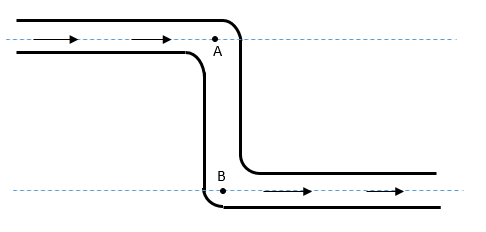
In the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities \[{v_A}\] and \[{v_B}\], and pressure \[{P_A}\]and \[{P_B}\] ​ at the points A and B respectively. Then;

A. \[{v_A} = {v_B}\]
B. \[{v_A} > {v_B}\]
C. \[{P_A} = {P_B}\]
D. \[{P_B} > {P_A}\]

Answer 1

Hint:The rate of flow of the liquid in a tube is constant and it is the product of the speed of flow and the area of cross-section. When there is pressure difference then the fluid starts flowing in the direction from the region of higher pressure to the lower pressure.

Formula used:
\[Q = Av\]
where Q is the rate of flow, A is the area of cross-section and v is the speed of flow.
\[P + \dfrac{{\rho {v^2}}}{2} + \rho gh = cons\tan t\],
This is called Bernoulli's theorem of conservation of energy.

Complete step by step solution:

Image: Liquid flows through the pipe

For the point A, let the velocity of flow is \[{v_A}\], the pressure is \[{P_A}\] and the area of cross-section is \[{A_A}\] and the height from the ground level is \[{h_A}\]. Then the rate of flow of fluid is,
\[{Q_A} = {A_A}{v_A}\]

For the point B, let the velocity of flow is \[{v_B}\], the pressure is \[{P_B}\] and the area of cross-section is \[{A_B}\] and the height from the ground level is \[{h_B}\]. Then the rate of flow of fluid is,
\[{Q_B} = {A_B}{v_B}\]

As the cross-section of the pipe is uniform throughout the length of the pipe,
\[{A_A} = {A_B}\]
And using the continuity equation, the rate of flow of the fluid at both the points is same,
\[{Q_A} = {Q_B}\]
\[\Rightarrow {A_A}{v_A} = {A_B}{v_B}\]
\[\Rightarrow {v_A} = {v_B}\]

Now, using the Bernoulli’s equation for both the points, we get
\[{P_A} + \dfrac{{\rho v_A^2}}{2} + \rho g{h_A} = {P_B} + \dfrac{{\rho v_B^2}}{2} + \rho g{h_B}\]
\[\Rightarrow {P_A} = {P_B} + \rho g\left( {{h_B} - {h_A}} \right)\]
\[\Rightarrow {P_A} = {P_B} + \rho g\left( {0 - {h_A}} \right)\]
\[\Rightarrow {P_A} = {P_B} - \rho g{h_A}\]
\[\therefore {P_A} < {P_B}\]
So, the pressure at point B is greater than pressure at A.

Therefore, the correct option is D.

Note: The gravitational potential energy of the fluid at A is greater than the gravitational potential energy of the fluid at B. when the fluid moves from A to B then the gravitational potential energy transformed to the pressure energy of the fluid because the kinetic energy is same at both the points. And hence, the energy at both the points is the same.