Question

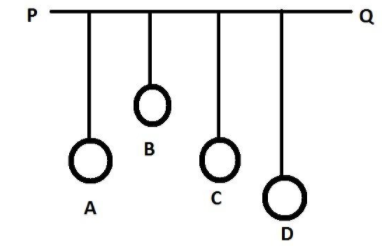
In the diagram A,B,C,D are four pendulums suspended from the same elastic string PQ. The length of A and C are equal to each other while the length of pendulum B is smaller than that of D. Pendulum A is set into a mode of vibrations.
(i) Name the type of vibrations taking place in pendulums B and D?
(ii) What is the state of pendulum C?
(iii) State the reason for the type of vibrations in pendulums B and C.

Answer 1

Hint: When a body executes vibrations under the action of an external periodic force, then the vibrations are called forced vibrations. The length of pendulum C is the same as that of A. Thus both remain in the same phase.

Complete step by step solution:
It has been given that, A,B,C,D are four pendulums suspended from the same elastic string PQ. The length of A and C are equal to each other while the length of pendulum B is smaller than that of D. Pendulum A is set into a mode of vibrations.
The vibrations that occur in the pendulums B and D are called forced vibrations. When a body oscillates by being influenced by an external periodic force, it is called forced oscillation. Here, the amplitude of oscillation experiences damping but remains constant due to the external energy supplied to the system.
Four pendulums A, B, C and D are suspended vertically from the horizontal support PQ. Lengths of A and C are equal and hence their individual frequency of oscillations are equal. Pendulum A is now displaced to one side and hence set into motion. After some time, pendulum C starts vibrating and soon gains some amplitude. After some time, all energy of A is transferred to C and vibration amplitude of C becomes maximum while that of A is minimum. The exchange of energy takes place continuously. Other pendulums also oscillate with a smaller magnitude.
The pendulum C has its length the same as that of A therefore its natural time period is also the same that of A and both remain in the same phase; so resonance takes place. But the length of B is less than the length of A.

Hence B would vibrate with smaller amplitude.

Note: There are three main types of Simple Harmonic Motion- Damped Oscillation, Forced Oscillation and Free Oscillation.
The free oscillation possesses constant amplitude and period without any external force to set the oscillation. Ideally, free oscillation does not undergo damping. But in all-natural systems damping is observed unless and until any constant external force is supplied to overcome damping. In such a system, the amplitude, frequency, and energy all remain constant.
The damping is a resistance offered to the oscillation. The oscillation that fades with time is called damped oscillation. Due to damping, the amplitude of oscillation reduces with time. Reduction in amplitude is a result of energy loss from the system in overcoming external forces like friction or air resistance and other resistive forces. Thus, with the decrease in amplitude, the energy of the system also keeps decreasing.