Question

In the above-shown figure, the direction of the magnetic force and magnetic field is given then find out the direction of the particle velocity v.
          
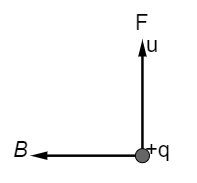
A) To the right.
B) Downward in the plane of the page
C) Upward in the plane of the page
D) Out of the plane of the page
E) Into the plane of the page.

Answer 1

Hint: For the motion of a charged particle in a magnetic field, the magnetic field vector $B$, the velocity of the particle vector $v$, and the magnetic force vector $F$ that exerted on the particle are all perpendicular to each other.

Complete answer:
The right-hand rule of Fleming states that, to find the direction of the magnetic force on a positive charge, the thumb of the right-hand point in the direction of the velocity of the particle $v$, the fingers in the direction of the magnetic field ($B$), and the force ($F$) is directed perpendicular to the right-hand palm.

The magnetic force on a charged particle with positive charge $q$ moving in a magnetic field $B$ with a velocity $v$ (at angle $\theta $ to $B$) is –
\[\overrightarrow F = qvB\sin \theta \]
\[ \Rightarrow \overrightarrow F = q(\overrightarrow v \times \overrightarrow B )\]
Therefore we can say, force is the cross product of $B$ and $v$ and hence Force is in the perpendicular plane of velocity and magnetic field.
Hence In the figure,

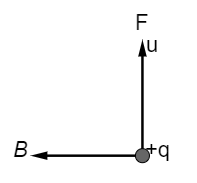
the direction of the magnetic field and force are given. Now if we apply Fleming right-hand rule the direction of the particle velocity will be into the plane of the page.

Hence, the option (E) is the correct answer.

Note: Fleming's rules are applied for determining the relation between the directions of magnetic field, electric current and velocity of a conductor.
There are two rules,
Fleming's left-hand rule for motors which applies for an electric current induces motion in the conductor in the presence of magnetic fields known as Lorentz force.
Fleming's right-hand rule for generators, which applies for a conductor moving through a magnetic field, has an electromotive force induced in it as a result known as Faraday's law of induction.