Question

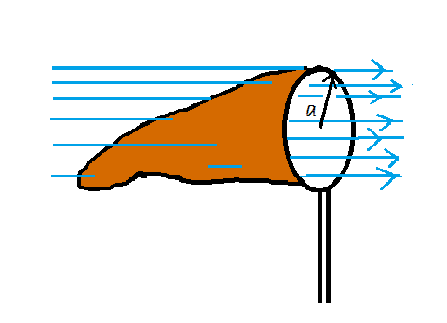
In figure, a butterfly net is in a uniform electric field of magnitude $E=3.0mN/C$. The rim, a circle of radius $a=11cm$, is aligned perpendicular to the field. The net contains no net charge. Find the electric flux through the netting.

Answer 1

Hint: We must know what is electric flux, what is the relation between electric flux and the electric field. For easier calculation of electric flux, we must be using a closed surface or we can make a closed surface and set the normal to the surface accordingly.

Formula used:
${{\varphi }_{flux}}=\oint{}\vec{E}\cdot d\vec{A}$

Complete step by step solution:
Definition of electric flux: Electric flux is the measure of the electric field through a given surface, although an electric field in itself cannot flow.
Relation between electric flux and electric field is given by:
${{\varphi }_{flux}}=\oint{}\vec{E}\cdot d\vec{A}$ .
The electric field is flowing in the positive x-direction. The outward normal is in the direction of the electric field, i.e. positive x-direction.
For easier calculation of electric flux, we can close the net by assuming that there is a disc of radius $a$ on the rim of the net. For the disc, the outward normal according to the electric field will be in the negative x-direction.
Hence,
${{\varphi }_{flux}}=\oint{}\vec{E}\cdot d\vec{A}$
Substituting, $\vec{E}=3.0mN/C=0.003N/C{\text{(}}\because {\text{1mN/C = 0}}{\text{.001N/C)}}$
\[{\varphi _{flux}} = - \oint {0.003 \times dA} \]
Area of the disc, $A = \pi {a^2}$where, $a = 11cm = 0.11m{\text{ (}}\because {\text{1cm = 0}}{\text{.01m)}}$
$\Rightarrow {{\varphi }_{flux,disc}}=-0.003\times \pi {{\left( 0.11 \right)}^{2}}$
$\Rightarrow {{\varphi }_{flux,disc}}=-3.63\pi \times {{10}^{-5}}N{{m}^{2}}/C$
$\Rightarrow {{\varphi }_{flux,net}}=-{{\varphi }_{flux,disc}}$
$\Rightarrow {{\varphi }_{flux,net}}=3.36\pi \times {{10}^{-5}}N{{m}^{2}}/C$

Therefore, the electric flux is $3.36\pi \times {{10}^{-5}}N{{m}^{2}}/C$.

Note: We must always make any open surface to the closed surface as it will make the calculation very easy. If a closed surface is given in the first place in the question itself, then the electric flux will be zero, unless there is some charge inside the closed surface. Sometimes, the flux will be zero even if there is a charge in the closed surface itself. In this case, the charges might be canceling each other. Hence, if the net charge contained in a closed surface is zero, then the flux due to the charges inside the closed surface will be zero.