Question

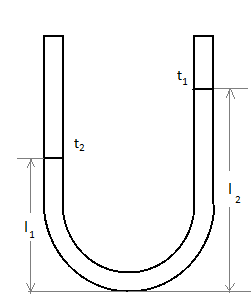
In a vertical U-tube containing a liquid, the two arms are maintained at different temperatures \[{t_1}\] and \[{t_2}\]. The liquid columns in the two arms have heights \[{l_1}\] and \[{l_2}\] respectively. The coefficient of volume expansion of liquid is equal to:

(A) \[{\dfrac{{{l_1} - {l_2}}}{{{l_2}{t_1} + {l_1}t}}_2}\]
(B) \[{\dfrac{{{l_1} - {l_2}}}{{{l_2}{t_1} - {l_1}t}}_2}\]
(C) \[{\dfrac{{{l_1} + {l_2}}}{{{l_2}{t_1} + {l_1}t}}_2}\]
(D) \[{\dfrac{{{l_1} + {l_2}}}{{{l_1}{t_1} + {l_2}t}}_2}\]

Answer 1

Hint: In any question involving U-tube, at first the pressure on both the arms must be balanced. In this case, after balancing the pressure on two legs apply the required conditions of volume expansion and thus obtain the coefficient of volume expansion of the liquid.

Complete step by step solution:
In a U-tube, when pressure is applied the height of liquid at the two limbs are unequal.
Let us consider, in the beginning that the pressure in both the limbs are equal:
Thus, the pressure in the limbs are balanced, so we write:
\[{p_o} + {\rho _{t_2}}g{l_2} = {p_o} + {\rho _{t_1}}g{l_1}\]
Where,
\[{p_o} = \] Atmospheric Pressure.
\[{\rho _{t_2}} = \]Density of liquid at temperature\[{t_2}\].
\[g = \] Acceleration due to gravity.
\[{l_2} = \]Length of second limb.
\[{\rho _{t_1}} = \] Density of liquid at \[{t_2}\].
\[{l_1} = \] Length of first limb.
On cancelling the common terms from sides:
\[{\rho _{t_2}}{l_2} = {\rho _{t1}}{l_1}\]
We know, due to change in temperature, the density of the liquid changes.
Now, let us consider \[{\rho _o}\] to be the initial density of the liquid.
Now, applying the formula that equates density to temperature, we know:
\[{\rho _{t_2}} = \dfrac{{{\rho _o}}}{{1 + \gamma {t_{_2}}}}\]
And, \[{\rho _{t_1}} = \dfrac{{{\rho _o}}}{{1 + \gamma {t_{_1}}}}\]
Where, \[\gamma = \] Coefficient of volume expansion.
When there is a change in volume of a liquid on application of heat (rise or reduction in temperature), the ratio of increase in volume with respect to per degree rise in temperature is known as coefficient of volume expansion.
Putting the values of \[{\rho _{t_1}}\] and \[{\rho _{t_2}}\]in the equation:
\[\dfrac{{{\rho _o}}}{{1 + \gamma {t_{_1}}}}.{l_1} = \dfrac{{{\rho _o}}}{{1 + \gamma {t_2}}}.{l_2}\]
Again, cancelling the common terms and cress multiplying the terms:
\[(1 + \gamma {t_2}){l_1} = (1 + \gamma {t_1}){l_2}\]
On further arranging the equation, we arrive at:
\[({l_1} - {l_2}) = \gamma ({l_2}{t_1} - {l_1}{t_2})\]
Thus,
\[\gamma = {\dfrac{{{l_1} - {l_2}}}{{{l_2}{t_1} - {l_1}t}}_2}\]

Therefore, option (B) is the correct answer.

Note: In case of U-tube, when positive pressure is applied in one leg of the U-tube, the liquid level in that particular limb decreases whereas the liquid level in the opposite level increases. U-tubes are widely used to measure pressure losses and difference in pressure in an industrial level. Usually mercury is used to measure pressure difference with U-tube manometers.