Question

In a conical pendulum, the axial height of a right circular cone described by the string is $\sqrt 3$ times the radius of the circular path of its bob. The tension in the string is:
A) \[2{\text{ }}mg\]
B) $\sqrt {3mg} $
C) $\dfrac{2}{{\sqrt 3 }}mg$
D) $\dfrac{1}{{\sqrt 3 }}mg$

Answer 1

Hint: A conical pendulum is a string with a mass attached at the end. The mass moves in a horizontal circular path and forms a right circular cone.A right circular cone is a cone where it’s axis is the line meeting the vertex to the midpoint of the radius of the circle. The center point of the base of the circle is joined with the apex of the cone and it forms a right angle.


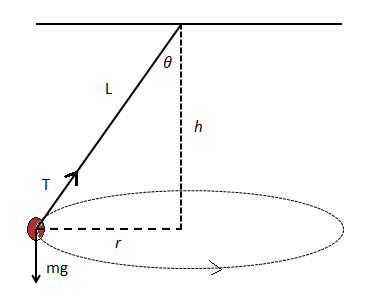
Formula used:
\[T\cos \theta = mg\]
Here, $T$ = tension created in the string
$r$ =radius of the circular path
$h$ = Axial height of the right circular cone
$l$ = height of the right circular cone that is slightly slant.
$mg$ = weight of the bob
$\theta $= $h$ and the string angle in between them measured in degrees

Complete step by step answer:
Let us consider the given tension diagram.

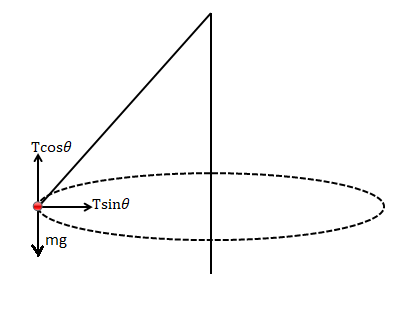
Here we divide the tension $T$ into two components that is a vertical and a horizontal.
The horizontal component is \[ = Tsin\theta \]
The vertical component \[ = Tcos\theta \].
So, according to the diagram,
\[T\cos \theta = mg\], where \[\cos \theta = \dfrac{h}{L}\]
Given, \[h = \sqrt 3 r\]
\[\therefore L = \sqrt {{r^2} + {{(\sqrt 3 r)}^2}} \] this can also be written as:
\[ \Rightarrow L = \sqrt {{r^2} + 3{r^2}} \]
Or,
\[ \Rightarrow L = \sqrt {4{r^2}} \]
Or,
\[ \Rightarrow L = 2r\]
So from,
\[T\cos \theta = mg\]
\[ \Rightarrow T = \dfrac{{mg}}{{\cos \theta }}\]
\[ \Rightarrow T = \dfrac{{mg}}{{\dfrac{h}{l}}}\]
\[ \Rightarrow T = \dfrac{{mgl}}{h}\]
\[ \Rightarrow T = mg \times \dfrac{{2r}}{{\sqrt 3 r}}\]
\[\therefore T = \dfrac{2}{{\sqrt 3 }}mg\]
Therefore the tension of the string \[T = \dfrac{2}{{\sqrt 3 }}mg\].

Hence the answer is the option (C).

Note: When two or more objects that are in contact, they exert force on each other and this particular force is called a Tension. Tension is the force that acts along a medium of the rope especially where the force is carried. Since the tension does not cause any displacement, the work done in the tension is zero and it acts in the opposite direction of the gravity force.