Question

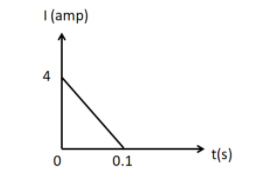
In a coil of resistance $10\Omega $, the induced current developed by changing magnetic flux through it, is shown in figure as a function of time. The magnitude of change in flux through the coil in Weber is-

(A) $2$
(B) $6$
(C) $4$
(D) $8$

Answer 1

Hint: To solve this question, we need to use Faraday's equation of the emf induced in a coil which is subjected to the changing magnetic flux. Then using the Ohm’s law, we can get the relation between the current and the rate of change in flux. On modifying that relation, we can get the expression for the change in flux.
Formula used: The formulae used in solving this question are given by
$e = - \dfrac{{d\varphi }}{{dt}}$, here $e$ is the emf induced in a coil, $\theta $ is the flux through the coil, and $t$ is the time.
$V = IR$, here $V$ is the voltage, $I$ is the current, and $R$ is the resistance.

Complete step-by-step solution:
We know from the Faraday’s law that the emf induced within a coil due to the changing magnetic flux through it is given by the equation
$e = - \dfrac{{d\varphi }}{{dt}}$
Taking the magnitude of the emf, we get
$e = \dfrac{{d\varphi }}{{dt}}$..................(1)
Now, from the Ohm’s law we know that
$V = IR$
Since the voltage across the coil will be equal to the emf induced across the coil, we substitute $V = e$ above to get
$e = IR$
From (1)
\[\dfrac{{d\varphi }}{{dt}} = IR\]
\[d\varphi = IRdt\]
Integrating both the sides, we get
\[\int {d\varphi } = \int {IRdt} \]
\[ \Rightarrow \Delta \varphi = \int {IRdt} \]
Since the radius of the coil is constant, we have
\[\Delta \varphi = R\int {Idt} \].....................(2)
We know that integration of a dependent variable with respect to the independent variable is basically the area under the curve of the dependent variable. So the value of the integrand in the above relation will be equal to the area of the triangle in the figure given in the question. We know that the area of a triangle is given by
$A = \dfrac{1}{2} \times b \times h$
According to the figure given, we have $A = \int {Idt} $, $b = 0.1s$, and $h = 4{\text{A}}$. Substituting these above we get
$\int {Idt} = \dfrac{1}{2} \times 0.1 \times 4$
$ \Rightarrow \int {Idt} = 0.2$.....................(3)
Putting (3) in (2), we get the magnitude of the emf induced as
\[\Delta \varphi = 0.2R\]
According to the question, the radius of the coil is $R = 10\Omega $. Substituting this above, we finally get
\[\Delta \varphi = 2{\text{ Wb}}\]
Thus, the magnitude of change in flux through the coil in Weber is equal to $2$.

Hence, the correct answer is option A.

Note: We could also find out the equation of the line for integrating it between the limits given in the figure. But that would have involved more calculations. If the curve was not a straight line, then we would have to perform integration by finding the equation of the curve.