
In a class of 60 students, 25 students play cricket, 20 students play tennis and 10 students play both the games, then the number of students who play neither are
(a). 0
(b). 35
(c). 45
(d). 25
Answer
522.3k+ views
Hint: Find the number of students who play both cricket and tennis by finding \[n\left( A\cup B \right)\]. From this the students who play neither cricket nor tennis can be formed by subtracting from total students.
Complete step-by-step answer:
Given the total number of students in a class = 60.
Let ‘A’ be the set of students who play cricket, which is 25 in number.
\[\therefore n\left( A \right)=25\]
Let ‘B’ be the set of students who play tennis, 20 in number.
\[\therefore n\left( B \right)=20\]
The number of students who play both cricket and tennis is 10.
\[\therefore n\left( A\cap B \right)=10\]
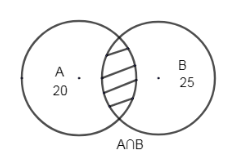
The shaded area shows \[A\cap B\].
The intersection of two sets A and B, consist of all elements that are both in A and B. The figure shows a Venn diagram representing the same.
Here, we are asked to find the number of students who don’t play cricket or tennis. Thus we need to find \[\left( A\cup B \right)\] and subtract it from the total number of students.
\[A\cup B\] is A union B, which means creating a new set containing every element from either of A and B.
The given Venn diagram represents \[A\cup B\].
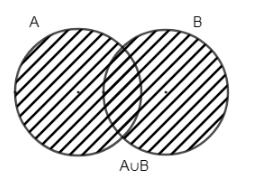
Hence, \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]
This formula can be directly derived from the above Venn diagram,
\[\therefore n\left( A\cup B \right)=25+20-10=35\].
Here, 35 students play at least one out of cricket or tennis out of 60 students in a class.
\[\therefore \]The number of students who play neither cricket nor tennis =
Total students – number of students who play at least one game
= Total students - \[n\left( A\cup B \right)\]
= 60 – 35 = 25
\[\therefore \]The number of students who play neither cricket nor tennis = 25.
Hence, option (d) is the correct answer.
Note: A Venn diagram is used to represent all possible relations of different sets. Here we used \[A\cap B\], which is the intersection of 2 sets to represent the common elements in both set A and B. And \[A\cup B\]represents the combined elements of set A and B.
Care should be taken not to confuse between \[A\cap B\] and \[A\cup B\].
Complete step-by-step answer:
Given the total number of students in a class = 60.
Let ‘A’ be the set of students who play cricket, which is 25 in number.
\[\therefore n\left( A \right)=25\]
Let ‘B’ be the set of students who play tennis, 20 in number.
\[\therefore n\left( B \right)=20\]
The number of students who play both cricket and tennis is 10.
\[\therefore n\left( A\cap B \right)=10\]

The shaded area shows \[A\cap B\].
The intersection of two sets A and B, consist of all elements that are both in A and B. The figure shows a Venn diagram representing the same.
Here, we are asked to find the number of students who don’t play cricket or tennis. Thus we need to find \[\left( A\cup B \right)\] and subtract it from the total number of students.
\[A\cup B\] is A union B, which means creating a new set containing every element from either of A and B.
The given Venn diagram represents \[A\cup B\].

Hence, \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]
This formula can be directly derived from the above Venn diagram,
\[\therefore n\left( A\cup B \right)=25+20-10=35\].
Here, 35 students play at least one out of cricket or tennis out of 60 students in a class.
\[\therefore \]The number of students who play neither cricket nor tennis =
Total students – number of students who play at least one game
= Total students - \[n\left( A\cup B \right)\]
= 60 – 35 = 25
\[\therefore \]The number of students who play neither cricket nor tennis = 25.
Hence, option (d) is the correct answer.
Note: A Venn diagram is used to represent all possible relations of different sets. Here we used \[A\cap B\], which is the intersection of 2 sets to represent the common elements in both set A and B. And \[A\cup B\]represents the combined elements of set A and B.
Care should be taken not to confuse between \[A\cap B\] and \[A\cup B\].
Recently Updated Pages
Graphical Methods of Vector Addition Explained Simply

Geostationary vs Geosynchronous Satellites: Key Differences Explained

Geometry of Complex Numbers Explained

JEE General Topics in Chemistry Important Concepts and Tips

Fusion Reaction in the Sun Explained: Simple Guide for Students

Functional Equations Explained: Key Concepts & Practice

Trending doubts
JEE Main 2026: Admit Card Out, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections (2025-26)

NCERT Solutions For Class 11 Maths Chapter 12 Limits and Derivatives (2025-26)

Derivation of Equation of Trajectory Explained for Students

Degree of Dissociation: Meaning, Formula, Calculation & Uses




