Question

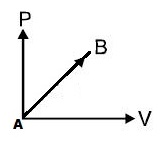
If work done by an ideal diatomic gas in a process from $\mathrm{A}$ to $\mathrm{B}$ as shown in $\mathrm{P}-\mathrm{V}$ graph is $20 \mathrm{J}$ :

Then increase in internal energy of the gas is:
(A) $40 \mathrm{J}$
(B) $60 \mathrm{J}$
(C) $100 \mathrm{J}$
(D) $120 \mathrm{J}$

Answer 1

Hint: We know that the internal energy is an extensive property: it depends on the size of the system, or on the amount of substance it contains. At any temperature greater than absolute zero, microscopic potential energy and kinetic energy are constantly converted into one another, but the sum remains constant in an isolated system. The internal energy of a system can be understood by examining the simplest possible system: an ideal gas. Because the particles in an ideal gas do not interact, this system has no potential energy. The internal energy of an ideal gas is therefore the sum of the kinetic energies of the particles in the gas.

Complete step by step answer
We know that the internal energy of an ideal gas is therefore the sum of the kinetic energies of the particles in the gas. The kinetic molecular theory assumes that the temperature of a gas is directly proportional to the average kinetic energy of its particles. All objects contain internal energy. ... When an object is heated, its particles move more vigorously and its internal energy increases. Unless the object changes state (e.g. melts or boils), its temperature will increase.
$\mathrm{W}=$ Area $=\dfrac{1}{2} \mathrm{P} \mathrm{V}=\dfrac{1}{2} \mathrm{nR} \Delta \mathrm{T}=20 \mathrm{J}$
Now the change in internal energy is given as $\dfrac{\mathrm{f}}{2} \mathrm{nR} \Delta \mathrm{T}$ (here $\mathrm{f}$ is the number of degree of freedom)
For a diatomic gas $f=5 .$ Thus we get $\Delta \mathrm{U}=\dfrac{5}{2} \mathrm{nR} \Delta \mathrm{T}=100 \mathrm{J} .=\mathrm{x}$
The number 100 is a perfect square and it has 9 factors including 1, 2, 4, 5, 10, 20, 25, 50 and 100

So the correct answers are option A and B.

Note: We know that the internal energy of a system is identified with the random, disordered motion of molecules; the total (internal) energy in a system includes potential and kinetic energy. The internal energy is the total amount of kinetic energy and potential energy of all the particles in the system. Whether the energy breaks bonds, increases the speed of the particles to stretch bonds, or just increases the speed of the particles depends on the temperature and state of the material. It depends on the quantity of a substance; hence it is extensive property. Change in it represents the heat evolved or absorbed in a reaction at constant temperature and constant volume.