Question

If we have a function as $f\left( x \right)={{x}^{3}}-6{{x}^{2}}-36x+2$ which is decreasing function, then x belongs to
A. \[\left( 6,\infty \right)\]
B. \[\left( -\infty ,-2 \right)\]
C. \[\left( -2,6 \right)\]
D. None of the above

Answer 1

Hint: We will be using the concept of polynomial specifically cubic equations to solve the problem. We will be using the concept of differential calculus to further simplify the solution.

Complete step-by-step solution -
Now, we have been given that $f\left( x \right)={{x}^{3}}-6{{x}^{2}}-36x+2$.
We have to find the domain for which the function is a decreasing function.
We know that the derivative of a function can be used to determine whether the function is decreasing or decreasing.
For a function to be decreasing we know $f'\left( x \right)<0$ for each point in an interval I.
For finding the interval in which the function is decreasing we have to first the critical points by $f'\left( x \right)=0$.
Now, we have $f\left( x \right)={{x}^{3}}-6{{x}^{2}}-36x+2$.
$\begin{align}
 \Rightarrow & f'\left( x \right)=3{{x}^{2}}-12x-36 \\
 \Rightarrow & 3{{x}^{2}}-12x-36=0 \\
\Rightarrow & 3\left( {{x}^{2}}-4x-12 \right)=0 \\
 \Rightarrow & {{x}^{2}}-6x+2x-12=0 \\
\Rightarrow & x\left( x-6 \right)+2\left( x-6 \right)=0 \\
\Rightarrow & \left( x+2 \right)\left( x-6 \right)=0 \\
\end{align}$
So, critical points are – 2, 6.
Now, we have to find for which range $f'\left( x \right)<0$. So, we will use the number line to show the critical points and find in which range $f'\left( x \right)<0$.

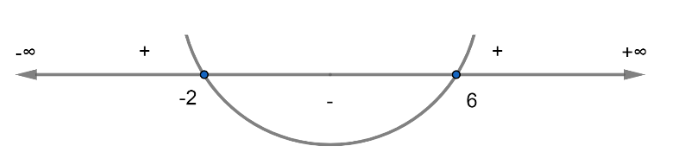
Now, for $x<-2\ and\ x>6$
$f'\left( x \right)>0$
Now, for $-2 < x < 6$
$f'\left( x \right)<0$
So, we have $f'\left( x \right)<0$ for $x\in \left( -2,6 \right)$.
Hence, the correct option is (C).

Note: To solve these types of questions it is important to know the concepts of inequality as we have used inequality to find the final answer, also it has to be noted that the function is decreasing if $f'\left( x \right) < 0$.