Question

If we given two unit vectors $\vec{a}\text{ and }\vec{b}$ such that, $\vec{a}+\vec{b}$ is also a unit vector, then find the angle between $\vec{a}\text{ and }\vec{b}$

Answer 1

Hint: To solve this question, we will use the given fact that, all the three vectors $\vec{a}\text{ and }\vec{b}\text{ and }\vec{a}\text{ + }\vec{b}$ are unit vectors. A vector is called unit vector if it has magnitude as 1. Also, if two vectors are $\vec{p}\text{ and }\vec{q}$ and angle between them is $\theta $ then
\[\vec{p}\cdot \vec{q}=\left| {\vec{p}} \right|\left| {\vec{q}} \right|\text{cos}\theta \]
Where $\left| {\vec{p}} \right|$ is magnitude of $\vec{p}$ and $\left| {\vec{q}} \right|$ is magnitude of $\vec{q}$
First we will use the fact that $\vec{a},\vec{b}\text{ and }\vec{a}\text{ + }\vec{b}$ are unit vectors and then we will use the formula of angle between two vectors stated above to get the answer.

Complete step-by-step solution:
Before starting the solution, let us first understand what a unit vector is. A vector is called a unit vector if the magnitude of it is 1. If $\vec{a}$ is a unit vector than $\left| a \right|=1$
Magnitude of a vector is the length of a vector. A vector $\vec{p}=x\hat{i}+y\hat{j}+z\hat{k}$ has its magnitude as $\left| {\vec{p}} \right|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$
Here given, $\vec{a}\text{ and }\vec{b}$ are both unit vector.
\[\Rightarrow \left| {\vec{a}} \right|=1\text{ and }\left| {\vec{b}} \right|=1\]
Also given that, $\vec{a}+\vec{b}$ is also a unit vector.
\[\Rightarrow \left| \vec{a}+\vec{b} \right|=1\]
If \[\left| {\vec{a}} \right|=1\] then squaring both sides \[\Rightarrow {{\left| {\vec{a}} \right|}^{2}}=1\]
Similarly, \[\left| {\vec{b}} \right|=1\Rightarrow {{\left| {\vec{b}} \right|}^{2}}=1\]
And \[\left| \vec{a}+\vec{b} \right|=1\Rightarrow {{\left| \vec{a}+\vec{b} \right|}^{2}}=1\]
Now, magnitude of a vector \[{{\left| {\vec{p}} \right|}^{2}}=\vec{p}\cdot \vec{p}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)}\]
Then, applying this logic on ${{\left| \vec{a}+\vec{b} \right|}^{2}}$ we get
\[\begin{align}
  & {{\left| \vec{a}+\vec{b} \right|}^{2}}=\left( \vec{a}+\vec{b} \right)\cdot \left( \vec{a}+\vec{b} \right)=1 \\
 & \Rightarrow \left( \vec{a}+\vec{b} \right)\cdot \left( \vec{a}+\vec{b} \right)=1 \\
\end{align}\]
Opening bracket of LHS of above equation:
\[\left( \vec{a}\cdot \vec{a} \right)+\left( \vec{a}\cdot \vec{b} \right)+\left( \vec{b}\cdot \vec{a} \right)+\left( \vec{b}\cdot \vec{b} \right)=1\]
Now, \[{{\left| {\vec{a}} \right|}^{2}}=1\] applying logic of equation (i)
\[\vec{a}\cdot \vec{a}=1\]
Similarly, \[{{\left| {\vec{b}} \right|}^{2}}=1\Rightarrow \vec{b}\cdot \vec{b}=1\]
Using this both values in above equation, we get:
\[\begin{align}
  & \Rightarrow 1+\vec{a}\cdot \vec{b}+\vec{b}\cdot \vec{a}+1=1 \\
 & \Rightarrow 2+2\vec{a}\cdot \vec{b}=1 \\
 & \Rightarrow \vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a} \\
\end{align}\]
Subtracting 2 both sides of above equation:
\[\begin{align}
  & \Rightarrow 2\left( \vec{a}\cdot \vec{b} \right)=1-2 \\
 & \Rightarrow 2\left( \vec{a}\cdot \vec{b} \right)=-1 \\
\end{align}\]
Dividing 2 both sides of above equation:
\[\Rightarrow \vec{a}\cdot \vec{b}=\dfrac{-1}{2}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}\]
Now, finally we will use the formula of angle between two vectors which is given as:
If two vectors are $\vec{p}\text{ and }\vec{q}$ then angle between them is $\theta $ then \[\vec{p}\cdot \vec{q}=\left| {\vec{p}} \right|\left| {\vec{q}} \right|\text{cos}\theta \]
Where $\left| {\vec{p}} \right|$ is magnitude of $\vec{p}$ and $\left| {\vec{q}} \right|$ is magnitude of $\vec{q}$
We have from equation (i) \[\Rightarrow \vec{a}\cdot \vec{b}=\dfrac{-1}{2}\]
Applying formula of angle between two vectors from above, supposing angle between $\vec{a}\text{ and }\vec{b}\text{ is }\theta $ we get:
\[\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta =\dfrac{-1}{2}\]
Now, \[\left| {\vec{a}} \right|=\left| {\vec{b}} \right|=1\text{ as }\vec{a}\text{ and }\vec{b}\] are unit vectors.
\[\begin{align}
  & \cos \theta =\dfrac{-1}{2}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iii)} \\
 & \Rightarrow \theta \text{=co}{{\text{s}}^{\text{-1}}}\left( \dfrac{-1}{2} \right) \\
\end{align}\]
We will use trigonometric identity as $\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $
\[\Rightarrow \cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta \]
From equation (ii) we have \[\cos \theta =\dfrac{-1}{2}\]
Substituting this in above:
\[\begin{align}
  & \Rightarrow \cos \left( {{180}^{\circ }}-\theta \right)=-\left( \dfrac{-1}{2} \right) \\
 & \Rightarrow \cos \left( {{180}^{\circ }}-\theta \right)=\dfrac{1}{2} \\
\end{align}\]
Now, value of $\cos {{60}^{\circ }}=\dfrac{1}{2}$
\[\Rightarrow \cos \left( {{180}^{\circ }}-\theta \right)=\cos {{60}^{\circ }}\]
Applying ${{\cos }^{-1}}$ both sides we get:
\[\begin{align}
  & \Rightarrow {{\cos }^{-1}}\left( \cos \left( {{180}^{\circ }}-\theta \right) \right)={{\cos }^{-1}}\left( \cos {{60}^{\circ }} \right) \\
 & \Rightarrow {{180}^{\circ }}-\theta ={{60}^{\circ }} \\
 & \Rightarrow \theta ={{180}^{\circ }}-{{60}^{\circ }} \\
 & \Rightarrow \theta ={{120}^{\circ }} \\
\end{align}\]
Therefore, angle $\theta $ between $\vec{a}\text{ and }\vec{b}\text{ is 12}{{\text{0}}^{\circ }}$
Hence, we have:

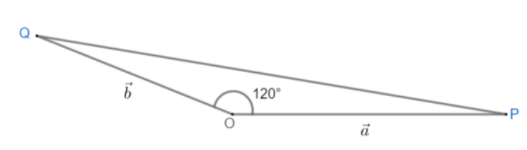
Where, \[OP=\vec{a}\text{ and OQ=}\vec{b}\]

Note: Solution can also end at a point where we got \[\cos \theta =\dfrac{-1}{2}\] by general trigonometric knowledge we have, that \[\cos {{120}^{\circ }}=\dfrac{-1}{2}\] so, we can directly get \[\theta ={{120}^{\circ }}\] but for more precise solution, we can also proceed by using trigonometric formula $\cos \left( {{180}^{\circ }}-\theta \right)=-\cos \theta $