Question

If the roots of ${x^2} + x + a = 0$ exceed $a$, then
A. $2 < a < 3$
B. $a > 3$
C. $ - 3 < a < 3$
D. $a < - 2$

Answer 1

Hint: Check the concavity of the given quadratic equation and using this information check whether $f(a)$ is positive or negative. Also use the fact that the discriminant must be greater than 0 as real roots exist. With the two inequalities, find the range of a.

Formula used: Discriminant of the standard quadratic equation $a{x^2} + bx + c = 0$ is ${b^2} - 4ac$

Complete step-by-step solution:
Let $f(x) = {x^2} + x + a$
The coefficient of ${x^2}$ in the equation ${x^2} + x + a = 0$ is greater than 0. Therefore, it is a concave upwards graph. Since it is a concave upwards graph, $f(x)$ will be negative only when $x \in \left[ {p,q} \right]$ where $p,q$ are the roots.

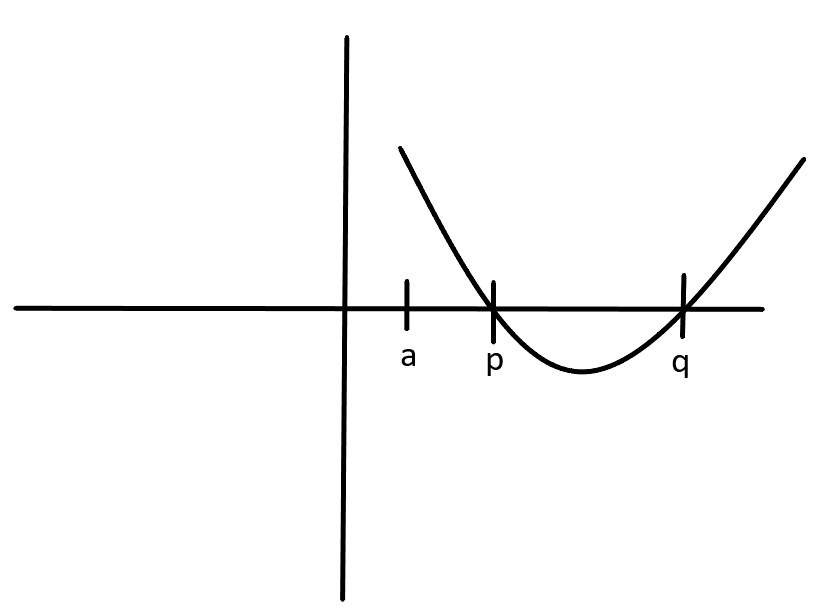
Therefore, $f(a)$ is positive. We also know that real roots exist. Therefore, the discriminant of the quadratic equation, ${x^2} + x + a = 0$ must also be greater than 0.
Since $f(a) > 0$,
${a^2} + a + a > 0$
${a^2} + 2a > 0$
$a(a + 2) > 0$
$a \in \left( { - \infty , - 2} \right) \cup \left( {0,\infty } \right)$
Since discriminant, $D > 0$,
$1 - 4a > 0$
$4a < 1$
$a < \dfrac{1}{4}$
$a \in \left( { - \infty ,\dfrac{1}{4}} \right)$
Taking the intersection of $\left( { - \infty , - 2} \right) \cup \left( {0,\infty } \right)$ and \[\left( { - \infty ,\dfrac{1}{4}} \right)\] we get $a \in \left( { - \infty , - 2} \right)$.
Therefore, the correct answer is option D. $a < - 2$.

Note: Given a quadratic polynomial $a{x^2} + bx + c$, if $a > 0$ then the graph of the quadratic polynomial will be a concave upwards graph and if $a < 0$ then the graph of the quadratic polynomial will be a concave downwards graph.