




How Does the Spring Force Formula Work in Practice?
Spring force governs how springs stretch or compress under applied loads, influencing countless engineering and daily-life mechanisms.
A spring force arises whenever a spring is either stretched or compressed away from its equilibrium (rest) position.
Think of pulling a door using its hinge springs; every inch you move it strains the spring, producing a resisting force called spring force.
This force always acts in the opposite direction to displacement, trying to restore the original shape of the spring.
According to Hooke's Law, the spring force is mathematically given by $F = -k(x - x_0)$. Here, $x$ is the current length, $x_0$ is the natural length, and $k$ is the spring constant.
The spring constant ($k$), crucial in the Spring Force Hooke's Law and Examples, represents the stiffness of the spring: stiffer springs have higher $k$ values.
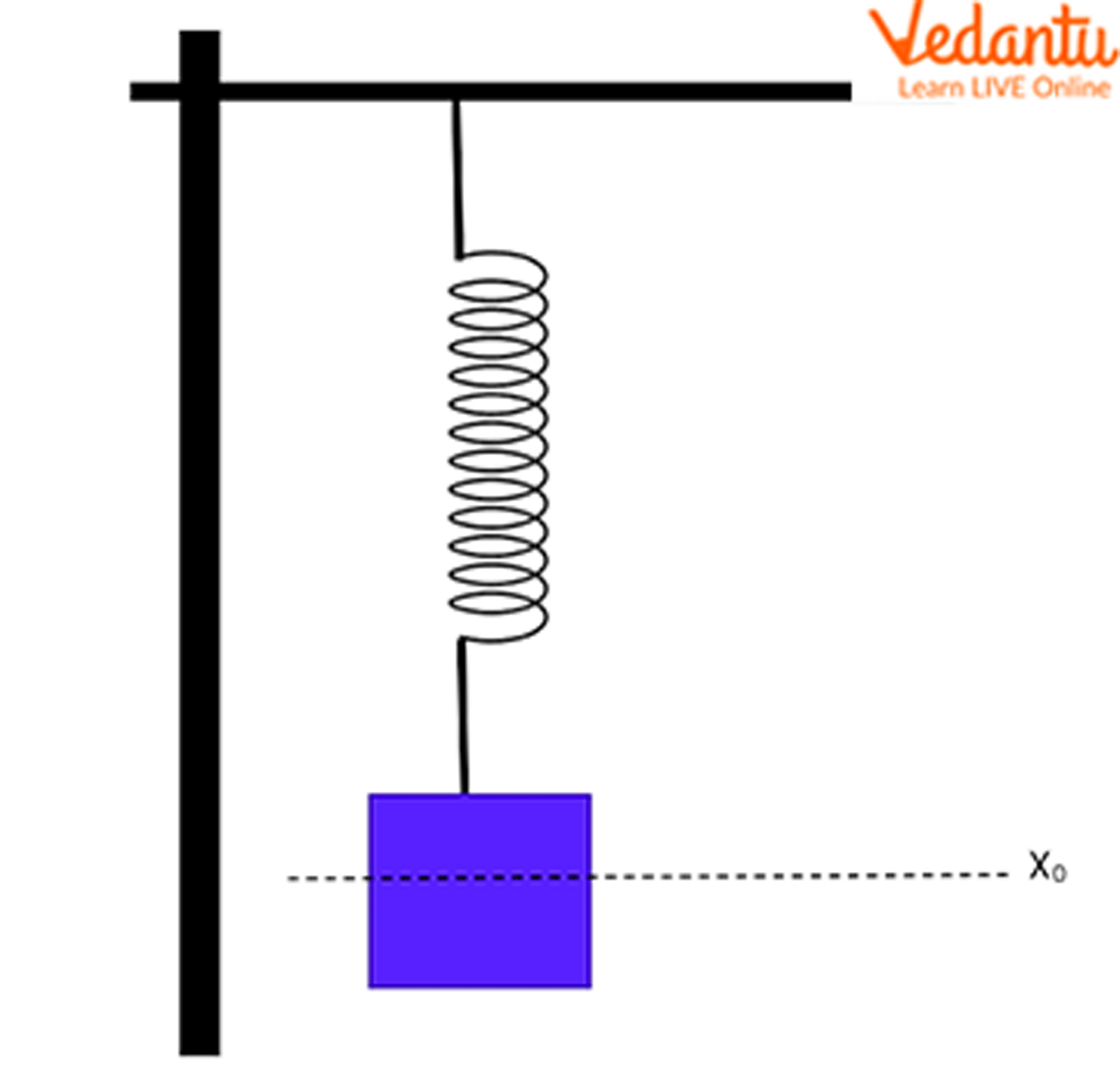
Stretch the spring by a displacement $x$, and the restoring force $F$ appears, trying to pull it back to its equilibrium.
If the spring is compressed, the force instead pushes outward, again seeking equilibrium; this is called restoring action.
You encounter spring force in watches, weighing balances, vehicle suspensions, and even trampolines.
Springs can be categorized by loading mode; for instance, the Spring Mass System analyzes oscillations when mass is attached to a vertical or horizontal spring.
- Compression springs resist being squashed
- Tension springs resist being stretched
- Torsion springs resist twisting forces
The SI unit of spring force is Newton (N), while the spring constant ($k$) is measured in Newtons per meter (N/m).
Engineers may use a spring force calculator for complex setups, but understanding fundamentals ensures accuracy during manual calculations.
Spring force is a classic example of a linear restoring force, essential in Kinematics and harmonic motion analysis.
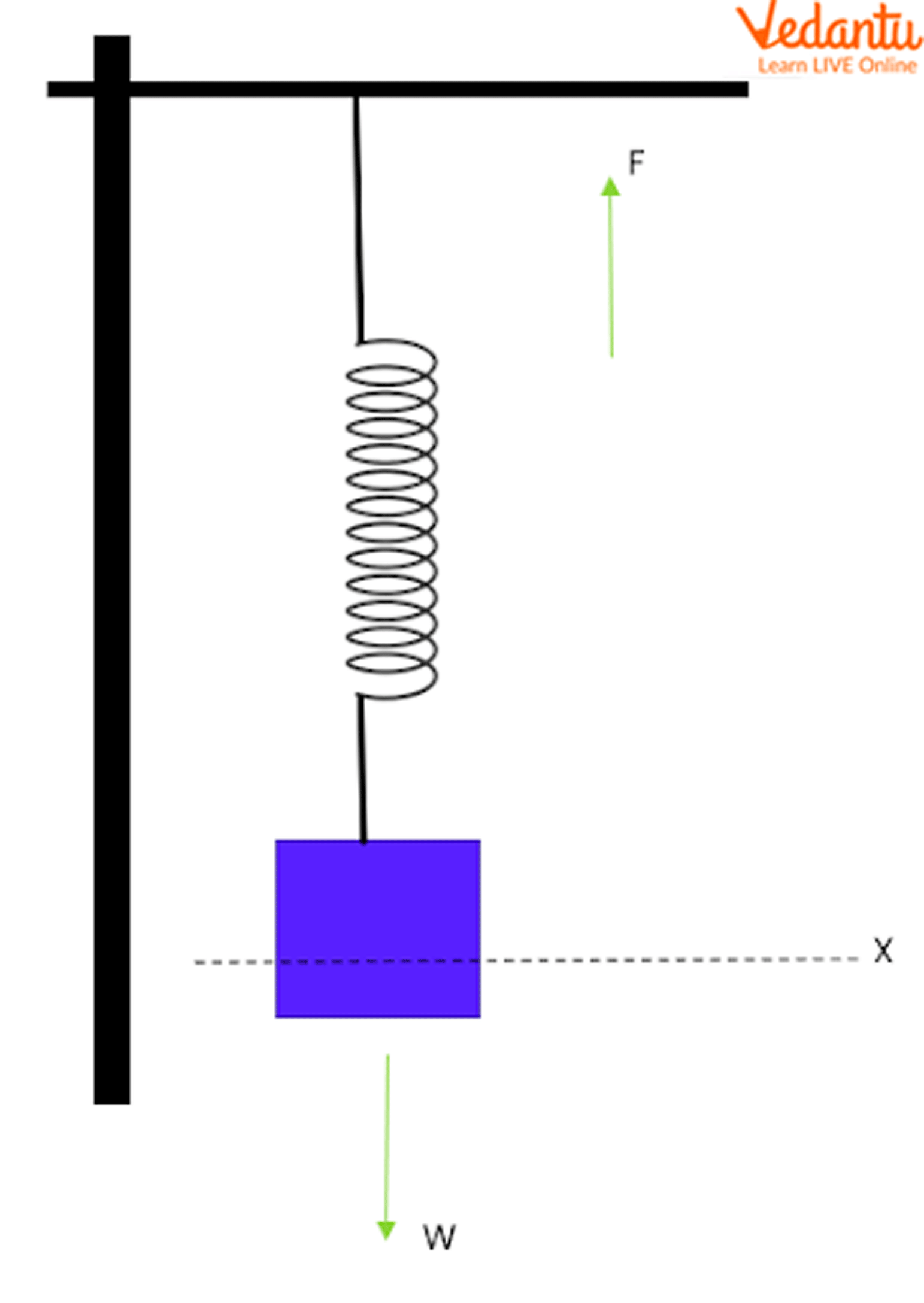
Consider a weight hanging from a spring. When displaced downward, spring force pulls upward, opposing the weight.
The equilibrium position is where these opposing forces balance. Deviations from this position initiate oscillatory motion.
To compare formulas and highlight application scope, review this compact table for reference:
| Parameter | Expression |
|---|---|
| Spring Force | $F = -k(x - x_0)$ |
| Elastic Potential Energy | $U = \dfrac{1}{2}k(x - x_0)^2$ |
| Work Done by Spring | $W = -\dfrac{1}{2}k(x_2^2 - x_1^2)$ |
The negative sign in $F = -k(x - x_0)$ emphasizes that the spring force always resists displacement, maintaining equilibrium.
You can see the effect of combined or series/parallel springs in advanced questions, often linking to the physics of Elastic Collision in Two Dimensions.
A frequently tested concept in JEE and NEET is the energy stored in a stretched or compressed spring, calculated as $U = \dfrac{1}{2}k(x - x_0)^2$.
- Spring force governs oscillations in pendulums and vibrations
- Helps explain energy conservation in mechanical systems
- Used in vehicle shock absorbers and mechanical clocks
Let us tackle a solved example: If a spring ($k = 200$ N/m) is stretched by 0.30 m from its rest length, what is the spring force?
Applying $F = -k(x - x_0)$, with $x - x_0 = 0.30$, we get $F = -200 \times 0.30 = -60$ N. The force is directed opposite to the stretch.
Practice question: If a spring's natural length is 40 cm and it is compressed to 35 cm with $k = 150$ N/m, calculate the spring force.
Diagrams help visualize that at every stage—compression, extension, or rest—a spring's restoring force is always directed toward the equilibrium position.
For oscillatory systems, the interplay between restoring spring force and inertia results in simple harmonic motion analyzed within Forces studies.
Overstretching a spring beyond its elastic limit will make it disobey Hooke's law, causing permanent deformation—often a common exam mistake.
JEE and NEET aspirants must not confuse equilibrium position ($x_0$) with zero force, as any displacement creates a nonzero restoring force.
For a deeper dive, the role of spring force in oscillations ties into potential and kinetic energies, as explored in Energy in SHM.
- Hooke's Law and its limitations
- Elastic potential energy in springs
- Spring-mass oscillators
- Series and parallel combinations of springs
- Work done by non-conservative forces
- Applications in measuring instruments
FAQs on What Is Spring Force? Understanding the Basics
1. What is spring force?
Spring force is the restoring force exerted by a spring when it is compressed or stretched from its equilibrium position.
- It always acts in the opposite direction to the displacement.
- Mathematically, it is given by Hooke’s Law: F = -kx, where F is the spring force, k is the spring constant, and x is the displacement.
2. State Hooke’s law.
Hooke’s law states that the force required to extend or compress a spring is directly proportional to the displacement within the spring’s elastic limit.
- Formula: F = -kx
- F = spring force (in newtons)
- k = spring constant (N/m)
- x = displacement from the natural length (in meters)
3. What are the SI units of spring constant?
The SI unit of the spring constant (k) is newton per meter (N/m).
- It represents the force required for unit displacement in the spring.
- Used in Hooke’s law calculations.
4. What factors affect the value of spring constant (k)?
The spring constant depends on several physical properties of the spring.
- Material: Stiffer materials have higher values of k.
- Length: Shorter springs generally have a higher k value.
- Coil thickness: Thicker wires result in greater k.
- Number of coils: More coils decrease the spring constant.
5. Is spring force a contact force? Why?
Yes, spring force is considered a contact force because it arises only when the spring is physically compressed or stretched by another object.
- There is direct contact between the spring and the object.
- The force disappears when contact is lost.
6. Give two practical applications of spring force in everyday life.
Spring force is used in many real-life devices.
- Shock absorbers in vehicles: Springs absorb impact forces and improve ride comfort.
- Mechanical watches: Springs store and gradually release energy to run the watch mechanism.
7. What happens if a spring is stretched beyond its elastic limit?
If a spring is stretched beyond its elastic limit, it gets permanently deformed and Hooke’s law no longer applies.
- The spring will not return to its original shape.
- The relationship between force and displacement becomes non-linear.
- This is called plastic deformation.
8. How does the orientation of a spring (vertical or horizontal) affect the spring force?
The orientation, whether vertical or horizontal, does not change the spring force calculation as per Hooke's law; however, gravity acts in vertical setups.
- Vertical: Weight of the object adds to the force on the spring.
- Horizontal: Only the applied force causes stretching or compression.
9. How do springs combine in series and parallel? What is the effective spring constant?
Springs in series and parallel combine differently, affecting the overall spring constant.
- Series: 1/keff = 1/k1 + 1/k2 + ...
- Parallel: keff = k1 + k2 + ...
- keff is the effective spring constant of the system.
10. What is the difference between elastic and plastic deformation in springs?
Elastic deformation means the spring returns to its original shape after the force is removed, following Hooke’s law.
Plastic deformation occurs when a spring is stretched beyond its elastic limit, causing permanent changes.
- Elastic: Temporary, reversible change.
- Plastic: Permanent, irreversible change.
























