Question

If the range of a projectile be R, then its kinetic energy is minimum when horizontal distance covered by it is
(A) $\dfrac{R}{4}$
(B) $\dfrac{R}{2}$
(C) $\dfrac{{3R}}{4}$
(D) R

Answer 1

Hint The velocity of the projectile motion changes at every position; kinetic energy is directly proportional to velocity which means that kinetic energy will be minimum when velocity is minimum. For a projectile motion the velocity is lowest when it reaches the maximum height. And this height is half of the range. So, Kinetic energy is least when the horizontal distance covered by is halved.

Complete step-by-step solution
Range of the motion is dependent on velocity, so at a point where range is minimum when velocity is minimum telling us that kinetic energy is also minimum at this point. Range is given by
 $R = \dfrac{{{v^2}\sin 2\theta }}{g}$
Kinetic energy is given by,
 $K = \dfrac{1}{2}m{v^2}$

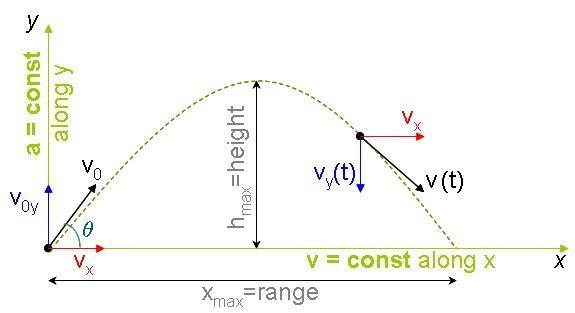
In the projectile motion of an object, it travels with a velocity v which is instantaneous. The velocity is minimum at the top of the projectile that is at the maximum height the velocity is going to be minimum indicating that the kinetic energy is also minimum.
The maximum height is at half of the range meaning at $\dfrac{R}{2}$ the max height is achieved where velocity is lowest.
Hence the kinetic energy is minimum when velocity is minimum at maximum height where the range is $\dfrac{R}{2}$ .

The correct option is B.

Note When a projectile moves upwards its kinetic energy decreases and potential energy increases but the total energy is always constant. This is in accordance with the law of conservation of energy. The kinetic energy of the projectile motion is maximum at the place of projection where velocity is max while potential energy is max at highest point.