Question

If \[\cos^{ - 1}\left( {\dfrac{1}{x}} \right) = \theta \]. Then what is the value of \[\tan\theta \]?
A. \[\dfrac{1}{{\sqrt {{x^2} - 1} }}\]
B. \[\sqrt {{x^2} + 1} \]
C. \[\sqrt {1 - {x^2}} \]
D. \[\sqrt {{x^2} - 1} \]

Answer 1

Hint: Use the given trigonometric equation and find the value of \[\cos \theta \]. Then using the Pythagoras theorem in a right-angled triangle, get the value of \[\sin \theta \]. In the end, take the ratio of \[\sin \theta \] to \[\cos \theta \] and get the required answer.

Formula used:
\[\sin A = \dfrac{{Opposite Side}}{{Hypotenuse}}\]
\[\cos A = \dfrac{{Adjacent Side}}{{Hypotenuse}}\]
\[\tan A = \dfrac{{Opposite Side}}{{Adjacent Side}} = \dfrac{{\sin A}}{{\cos A}}\]
Pythagoras Theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Complete step by step solution:
The given trigonometric equation is \[\cos^{ - 1}\left( {\dfrac{1}{x}} \right) = \theta \].
Let’s simplify the given equation.
\[\cos \theta = \dfrac{1}{x}\] \[.....\left( 1 \right)\]

Now substitute the value of \[cos \theta \] in a right-angled triangle.

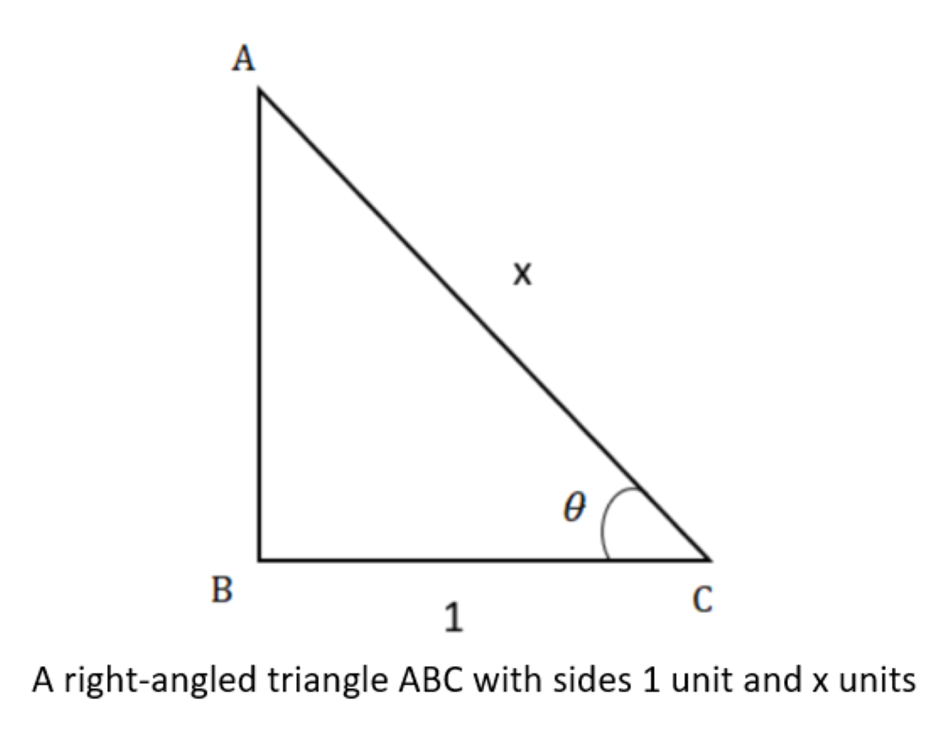
Apply Pythagoras theorem to calculate the length of \[AB\].
\[{\left( {AB} \right)^2} + {\left( {BC} \right)^2} = \left( {AC} \right){}^2\]
Substitute the values from the above triangle.
\[{\left( {AB} \right)^2} + {\left( 1 \right)^2} = \left( x \right){}^2\]
\[ \Rightarrow \]\[{\left( {AB} \right)^2} = x{}^2 - 1\]
Take square root of both sides.
\[AB = \sqrt {x{}^2 - 1} \]
Now use the trigonometric ratio and find the value of \[\sin \theta \].
\[\sin \theta = \dfrac{{\sqrt {{x^2} - 1} }}{x}\] \[.....\left( 2 \right)\]
Apply the trigonometric ratio \[\tan A = \dfrac{{\sin A}}{{\cos A}}\].
\[\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}\]
Substitute equation \[\left( 1 \right)\] and \[\left( 2 \right)\] in the above equation.
\[\tan \theta = \dfrac{{\dfrac{{\sqrt {{x^2} - 1} }}{x}}}{{\dfrac{1}{x}}}\]
\[ \Rightarrow \]\[\tan \theta = \dfrac{{\sqrt {{x^2} - 1} }}{1}\]
\[ \Rightarrow \]\[\tan \theta = \sqrt {{x^2} - 1} \]
Hence the correct option is D.

Note: Trigonometry is based upon the ratios of the sides of a right triangle. These ratios are called trigonometric ratios. Three common trigonometric ratios are the sine, cosine, and tangent.