Question

If a parallel beam of light of circular cross-section having radius $10mm$ falls on the surface of glass slab $(\mu = \dfrac{3}{2})$ at an angle of ${30^0} $, then the radius of the refracted beam is about:
A) $12.5mm$
B) $13.7mm$
C) $14.5mm$
D) $16.2mm$

Answer 1

Hint: The refractive index of a substance depends on the optical frequency or wavelength; this dependence is called chromatic dispersion. Typical refractive index values for glasses and crystals (e.g. laser crystals) in the visible spectral region are in the range from $1.4$ to $2.8$, and usually the refractive index rises for shorter wavelengths (normal dispersion). That is because the strongly transmitted spectral region lies between the spectral areas of heavy absorption: the ultraviolet zone with photon energies above the energy gap and the close or mid infrared field with vibrational resonance and its overtones.

Complete step by step solution:
As light, e.g. a laser beam, extends from a translucent homogeneous medium to another, the direction of its spread is usually different. This is what refraction is called. It comes from the border conditions that must be met at the border of the two media by the input and transmitted signal. Essentially, the wave vector tangential components must be the same since otherwise the difference in phase between the waves at the border will be positional, and the wave fronts cannot proceed. As the size of the wave vector depends on the medium refractive index, in general, this condition can only be accomplished by various directions of propagation.

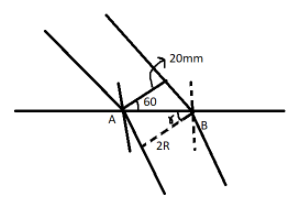
From the above given figure,
It is given that the refractive index or $\mu = \dfrac{3}{2} $
$ \Rightarrow \dfrac{3}{2}\sin \gamma = \sin {60^0} $
$\sin \gamma = \dfrac{1}{{\sqrt 3}} $
Therefore,
$ \Rightarrow \cos \gamma = \sqrt {\dfrac{2}{3}} $
From the figure given,
$ \Rightarrow \cos 60 = \dfrac{{20}}{{AB}}$
$ \Rightarrow \cos \gamma = \dfrac{{2R}}{{AB}} $
Dividing the above two equations on the right and left sides, we get,
$ \Rightarrow \dfrac{{\cos \gamma}}{{\cos 60}} = \dfrac{R}{{10}}$
$ \Rightarrow \dfrac{{2\sqrt 2}} {{\sqrt 3}} = \dfrac{R}{{10}} $
$ \Rightarrow R = \dfrac{{20\sqrt 2}} {{\sqrt 3}} $
$ \Rightarrow R = 16.2mm$

Therefore, the correct option is D.

Note: The group index, which quantifies the reduction of group velocity, is another type of index. Extreme excesses of the refractive index and especially of the Group Index are observed in some quantum optics experiments near sharp resonances. This can be correlated with incredibly large or small group speed values (slow light). An effective refractive index can be allocated according to its phase speed for wave guides in each propagation mode.