Question

${I_1}$ is the moment of inertia of a thin circular ring about its axis. The ring is cut at a point then it is unfolded into a straight road. If ${I_2}$ is the moment of inertia of the rod about an axis perpendicular to the length of the rod and passing through its center, then the ratio of ${I_1}$ to${I_2}$ is:
(A) $3:\pi $
(B) $3:{\pi ^2}$
(C) $4:\pi $
(D) $4:{\pi ^2}$

Answer 1

Hint: - Consider a small element of $dm$and of $dx$ length, which is at a distance of $x$ from the center of the rod. Assume that the rod has uniform mass density and find a relation between $dm$ and $dx$ . Then integrate for the limits from $x = - \dfrac{L}{2}$ to $x = \dfrac{L}{2}$ . Repeat the same procedure for the ring.
Formula used: $I = m{r^2}$

Complete step-by-step answer:
Let us first derive the expression for both the moments of inertia and then divide both to find the ratio.
Now, the axis of rotation is passing through the center of this ring and is perpendicular to the plane of the ring.
Consider the mass of the ring $M$. In this case, the mass $dm$ will be at a perpendicular distance to $R$ from the center.

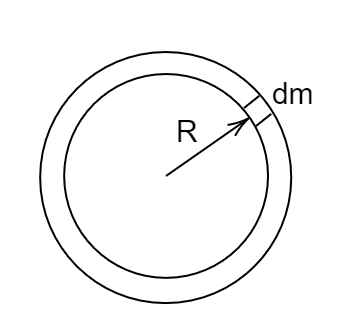
Therefore, $d{I_1} = dm{R^2}$
$ \Rightarrow {I_1} = \int {dm{R^2}} $
Here, $R$ is constant because the radius of the ring is fixed.
Therefore, ${I_1} = {R^2}\int {dm} = M{R^2}$ ........... $\left( 1 \right)$
Now, the ring is cut at a point then it is unfolded into a straight rod of length $L$ .
Here, $L = 2\pi R$ .......... $\left( 2 \right)$
Let the mass of the rod be $M$ and the length of the rod be $L$ .
For the moment of inertia ${I_2}$ of the rod about an axis perpendicular to its length and passing through its center of mass, again consider a small element of mass$dm$ . Let the length of this $dm$ mass be $dx$ and let it be a distance $x$ from the center of mass of the rod. Assume that the mass of the rod is uniformly distributed and hence the center of mass will be the center of the rod.

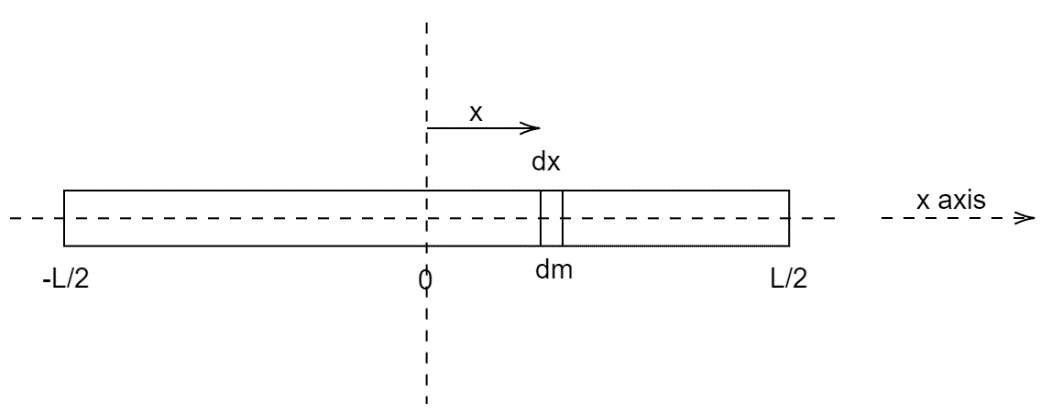
The Center of mass is defined as the product of the mass of the element and its perpendicular distance from the axis of rotation. Here the perpendicular is equal to $x$ . Let the moment of inertia of this element be $d{I_2}$.
Therefore, $d{I_2} = dm{x^2}$ ............. $\left( 3 \right)$
The mass of the rod is uniformly distributed, hence its mass density will be constant.
Therefore, $\dfrac{{dm}}{{dx}} = \dfrac{M}{L}$.
$ \Rightarrow dm = \dfrac{M}{L}dx$
Substitute the value of $dm$in equation $\left( 3 \right)$ .
$d{I_2} = \dfrac{M}{L}{x^2}dx$
Integrate both sides and keep the limits of $x$ from $ - \dfrac{L}{2}$ to $\dfrac{L}{2}$ .
$\int {d{I_2} = \int\limits_{ - \dfrac{L}{2}}^{\dfrac{L}{2}} {\dfrac{M}{L}{x^2}dx} } $
$ \Rightarrow {I_2} = \dfrac{M}{L}\int\limits_{ - \dfrac{L}{2}}^{\dfrac{L}{2}} {{x^2}dx} $
On integrating the above equation we get,
${I_2} = \dfrac{M}{L}\left[ {\dfrac{{{x^3}}}{3}} \right]_{\dfrac{{ - L}}{2}}^{\dfrac{L}{2}}$
On solving the limits we get,
${I_2} = \dfrac{M}{L}\left( {\dfrac{{{L^3}}}{{8 \times 3}} + \dfrac{{{L^3}}}{{8 \times 3}}} \right)$
$ \Rightarrow {I_2} = \dfrac{M}{L}\left( {\dfrac{{{L^3}}}{{12}}} \right) = \dfrac{{M{L^2}}}{{12}}$ ............. $\left( 4 \right)$
Divide equation $\left( 1 \right)$ and $\left( 4 \right)$ .
$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{M{R^2}}}{{\dfrac{{M{L^2}}}{{12}}}} = \dfrac{{12{R^2}}}{{{L^2}}}$ .
Substitute the value of $L$ from equation $\left( 2 \right)$ we get,
$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{12{R^2}}}{{{{\left( {2\pi R} \right)}^2}}} = \dfrac{{12{R^2}}}{{4{\pi ^2}{R^2}}}$
On further solving we get,
${I_1}:{I_2} = 3:{\pi ^2}$

Hence, the correct answer is option (B) $3:{\pi ^2}$ .

Note: it is not mentioned in the question, but we still have assumed that the rod has a uniform mass density. If the mass has a non-uniform density then the answer will be different. This means that $\dfrac{{dm}}{{dx}}$ is not always a constant value. Remember all the formulas of the moment of inertia of different bodies and both the theorems i.e. perpendicular axis theorem and parallel axis theorem.