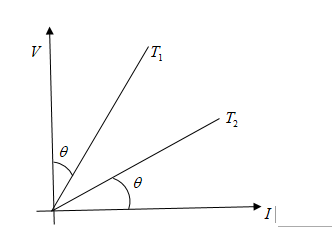
graph $$V - I$$ of a conductor at two different temperatures is shown in fig. the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ is:(A) ${\tan ^2}\theta $\t\t\tB) ${\cot ^2}\theta $\t\tC) ${\sec ^2}\theta $\t\tD) $\cos e{c^2}\theta $

Question

graph  $$V - I$$ of a conductor at two different temperatures is shown in fig. the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ is:(A) ${\tan ^2}\theta $\t\t\tB) ${\cot ^2}\theta $\t\tC) ${\sec ^2}\theta $\t\tD) $\cos e{c^2}\theta $

Vedantu Content Team · Accepted Answer

Hint  As we can see in the figure that $V$ and $I$ are making a right angle triangle, and ${T_1}$ is making angle $\theta $ with voltage and similarly ${T_2}$ is making $\theta $ angle with current. So, we apply trigonometry functions to solve this problem.Complete Step by step solutionAs per figure, we can see that${T_1} = \tan \theta $And ${T_2} = \tan \left( {90 - \theta } \right)$We know that the value of $\tan \left( {90 - \theta } \right)$will become $\cot \theta $Now, we can say that ${T_2} = \cot \theta $To find out the ratio of $\dfrac{{{T_1}}}{{{T_2}}}......(1)$We will put the values of ${T_1}$ and ${T_2}$in equation $(1)$$\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\tan \theta }}{{\cot \theta }}......(2)$We know that $\cot \theta  = \dfrac{1}{{\tan \theta }}$, we put it equation $(2)$$\dfrac{{{T_1}}}{{{T_2}}} = {\tan ^2}\theta $Hence, option a is the right answerNote We should keep in mind trigonometry formulas to solve this problem. As we know that $90 - \theta $means value will lies in first quadrant and in first quadrant $\tan \theta $ will convert in $\cot \theta $, so the value of $\tan \left( {90 - \theta } \right)$ will become $\cot \theta $Additional information $V - I$ graph stands for a graph of voltage and current, and it shows us properties of a conductor or device. $V - I$ Graph tells valuable information about the resistance in the circuit and breakdown of the electronic component. This information helps us place the electronic component in an electronic circuit. Voltage lies on $y - axis$ and current lies on $x - axis$, resistance tells us the type of the graph. If resistance is constant, the graph will be linear and if resistance is not constant means variable then the graph will be non-linear.There are different types of $V - I$ graphs, which are as below:Linear $V - I$ graph Non-linear $V - I$ graph$V - I$ Characteristics of SCR$V - I$ Characteristics of LED$V - I$ Characteristics of MOSFET$V - I$ Characteristics of PN Junction Diode$V - I$ Characteristics of Zener Diode

graph \[V - I\] of a conductor at two different temperatures is shown in fig. the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ is:
(A) ${\tan ^2}\theta $
B) ${\cot ^2}\theta $
C) ${\sec ^2}\theta $
D) $\cos e{c^2}\theta $

Repeaters Course for JEE 2022 - 23

graph \[V - I\] of a conductor at two different temperatures is shown in fig. the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ is:(A) ${\tan ^2}\theta $ B) ${\cot ^2}\theta $ C) ${\sec ^2}\theta $ D) $\cos e{c^2}\theta $

Repeaters Course for JEE 2022 - 23

graph \[V - I\] of a conductor at two different temperatures is shown in fig. the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ is:
(A) ${\tan ^2}\theta $
B) ${\cot ^2}\theta $
C) ${\sec ^2}\theta $
D) $\cos e{c^2}\theta $