Question

Four point charges $Q,\,q,\,Q\,$ and $q$ are placed at the corners of the square of a side $'a'$ as shown in the figure.

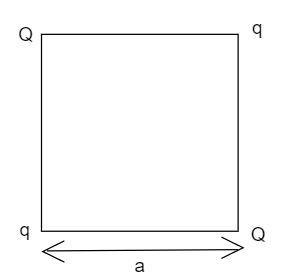
Find the:
(a) Resultant electric force on a charge $Q$ , and
(b) Potential energy of this system.

Answer 1

Hint: Use the formula of the electrical force between two charges and substitute the known parameters to find the electric force on $Q$. To find the potential energy of the system, find the potential energy between the two charges and add all the potential energies.

Useful formula:
(1) The electric force on the charge is given by
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Where $k$ is the coulomb constant, ${q_1}$ and ${q_2}$ are the charges under consideration and $r$ is the distance between the charges.

(2) The potential energy of two charges is given by
$P = \dfrac{{k{q_1}{q_2}}}{r}$
Where $P$ is the potential energy of two charges.

Complete step by step solution:
It is given that the
Distance between the charges, $r = a$
(a) To find the electric force on the charge $Q$ , the formula (1) is taken.
 $F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
The force between the $Q$ and the $Q$ is calculated.
${F_{QQ}} = \dfrac{{k{Q^2}}}{{2{a^2}}}$
Similarly the force between the $Q$ and the other charges are calculated.
${F_{Qq}} = \sqrt 2 \dfrac{{kqQ}}{{{a^2}}}$
The resultant electric force on the charge $Q$ is the sum of the electric force provided by the other charges.
$F = {F_{QQ}} + {F_{Qq}}$
${F_{}} = \sqrt 2 \dfrac{{kqQ}}{{{a^2}}} + \dfrac{{k{Q^2}}}{{2{a^2}}}$
By simplifying the above equation,
$F = \dfrac{{2\sqrt 2 kqQ + k{Q^2}}}{{2{a^2}}}$
By taking the common terms out of the brackets,
$F = \dfrac{{kQ}}{{2{a^2}}}\left( {2\sqrt 2 q + Q} \right)$
Hence the resultant of the electric force that acts on the charge $Q$ is $\dfrac{{kQ}}{{2{a^2}}}\left( {2\sqrt 2 q + Q} \right)$ .

(b) Use the formula (2),
$P = \dfrac{{k{q_1}{q_2}}}{r}$
The total potential energy is the sum of the potential energies between all the charges.
$P = {P_{QQ}} + {P_{Oq}} + {P_{qq}}$
$P = \dfrac{{k{q_1}{q_2}}}{r} + \dfrac{{k{q_1}{q_2}}}{r} + \dfrac{{k{q_1}{q_2}}}{r}$
Substituting the known values,
$P = \dfrac{{k{Q^2}}}{{\sqrt 2 a}} + \dfrac{{4kQq}}{a} + \dfrac{{k{q^2}^{}}}{{\sqrt 2 a}}$
Hence the potential energy of the system is obtained as $\dfrac{{k{Q^2}}}{{\sqrt 2 a}} + \dfrac{{4kQq}}{a} + \dfrac{{k{q^2}^{}}}{{\sqrt 2 a}}$.

Note: The distance between two points are in the hypotenuse side of the square, then it is calculated by the formula $\sqrt {\left( {{a^2} + {b^2}} \right)} $. For example the distance between $Q$ and $Q$ or $q$ and $q$ is calculated as $\sqrt {\left( {{a^2} + {a^2}} \right)} = \sqrt {2{a^2}} = \sqrt 2 a$.