Question

For the reaction, \[aA + bB\xrightarrow{{}}cC + dD\] , the plot of \[\log k\] vs \[1/T\] is given below:

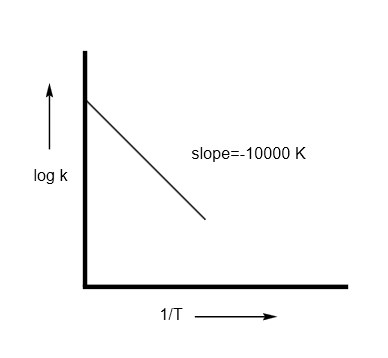
The temperature at which the rate constant of the reaction is \[{10^{ - 4}}{s^{ - 1}}\] is ______ \[K\] . [Rounded off to the nearest integer]
[given: the rate constant of the reaction is \[{10^{ - 5}}{s^{ - 1}}\] at \[500\,K\] ].

Answer 1

Hint: Here, in this question, a graph of \[\log k\] vs \[1/T\] is given. We have to use the Arrhenius equation for calculating the temperature.

Formula Used:
The Arrhenius equation is as follows:
\[k = A{e^{ - \dfrac{{{E_a}}}{{RT}}}}\]
Here, \[k\] is the rate constant of the reaction, \[A\] is the pre-exponential factor, \[e\] is the base of natural logarithm (Euler’s number), \[{E_a}\] is the activation energy of the chemical reaction in terms of energy per mole, \[R\] is universal gas constant, \[T\] is the absolute temperature associated with the reaction (in Kelvin).

Complete Step by Step Solution:
The Arrhenius equation is a formula that shows how the rate constant (of a chemical reaction), absolute temperature, and the A factor are related (also known as the pre-exponential factor; can be visualised as the frequency of correctly oriented collisions between reactant particles). It elucidates the relationship between response rates and temperature absolute.

From the Arrhenius equation, let us calculate the temperature as follows:
$ k = A{e^{ - \dfrac{{{E_a}}}{{RT}}}} \\$
$ \ln k = \ln A - \dfrac{{{E_a}}}{{RT}} \\$
$ 2.303 \times \log k = \left( {2.303 \times \log A} \right) - \dfrac{{{E_a}}}{{RT}} \\ $

Further solving,
\[\log k = \log A - \dfrac{{{E_a}}}{{2.303RT}}\]
Now, compare the above equation with the common equation of line \[y = mx + c\].
We get the value of slope,
$ slope = - \dfrac{{{E_a}}}{{2.303RT}} \\$
$ \Rightarrow - \dfrac{{{E_a}}}{{2.303RT}} = - 10000 \\$
$ \Rightarrow \dfrac{{{E_a}}}{{2.303RT}} = 10000 \\ $

From the Arrhenius equation,
$ \log \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{E_a}}}{{2.303R}} \times \left( {\dfrac{1}{{{T_1}}} - \dfrac{1}{{{T_2}}}} \right) \\$
$ \Rightarrow \log \dfrac{{{{10}^{ - 4}}}}{{{{10}^{ - 5}}}} = 10000 \times \left( {\dfrac{1}{{500}} - \dfrac{1}{{{T_{}}}}} \right) \\$
$ \Rightarrow 1 = 10000 \times \left( {\dfrac{1}{{500}} - \dfrac{1}{{{T_{}}}}} \right) \\ $

Further solving,
$ \dfrac{1}{{10000}} = \dfrac{1}{{500}} - \dfrac{1}{T} \\$
$ \Rightarrow \dfrac{1}{T} = \dfrac{1}{{500}} - \dfrac{1}{{10000}} \\$
$ \Rightarrow \dfrac{1}{T} = \dfrac{{20 - 1}}{{10000}} \\ $

Further solving,
$ \dfrac{1}{T} = \dfrac{{19}}{{10000}} \\$
 $ \Rightarrow T = \dfrac{{10000}}{{19}} \\$
$ \Rightarrow T = 526\,K \\ $

As a result, the temperature is \[526\,K\] at which the rate constant of the reaction is \[{10^{ - 4}}{s^{ - 1}}\] .

Note: Catalysts aid in decreasing the activation energy required for a specific reaction. As a result, the decreased activation energy accounted for by catalysts is substituted in the Arrhenius equation to obtain the catalysed reaction rate constant.