Question

Find $\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+{{x}^{x}}$ where $\left[ \cdot \right]$ is the G.I.F \[\]
A.1\[\]
B.2\[\]
C.0\[\]
D.$-1$\[\]

Answer 1

Hint: We find limit of the function $\left[ \dfrac{x}{\sin x} \right]$ by observing the curves of $x,\sin x$ within the closest interval to 0 that is $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$ where we get $x<\sin x,x<0$ and $x.\sin x,x>0$. We find the limit of other term by putting ${{x}^{x}}={{e}^{x\ln x}}$.

Complete step-by-step solution:
We know that limiting value for any real valued single variable function $f\left( x \right)$ when the variable $x$ approaches to real number $a$ in the domain $f\left( x \right)$ is denoted by
\[\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=L\]
Here $L$ is called the limit of the function.
The limit $L$ exists for real valued single variable function $f\left( x \right)$ at any point $x=a$ then if and only if Left hand limit(LHL)= right hand limit(RHL) at $x=a$. In symbols,
\[\begin{align}
  & \text{LHL}=\text{RHL} \\
 & \Rightarrow \underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right) \\
\end{align}\]
We know from the laws of limits for the limit for two real valued functions $f\left( x \right)$ and $g\left( x \right)$ at point $x=a$ for both functions then by law of addition in limits
\[\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)+\underset{x\to a}{\mathop{\lim }}\,g\left( x \right)=\underset{x\to a}{\mathop{\lim }}\,\left( f\left( x \right)+g\left( x \right) \right)\]
The given function to evaluate limit is .
$\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+{{x}^{x}}$
Where $\left[ \cdot \right]$ is the greatest integer function which returns the greatest integer smaller than or equal to that number. In symbols if $x\in \left[ m,n \right]$ where $ m < n $ are integers, then
We can use the law of addition to separate the limits and get,
\[\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+{{x}^{x}}=\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+\underset{x\to 0}{\mathop{\lim }}\,{{x}^{x}}....(1) \]
Let us investigate the first limit. We know that $x$ is in radian and we observe the closest interval to 0 where the function starts approaching without increasing or decreasing that is $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]=\left[ \dfrac{-3.14}{2},\dfrac{3.14}{2} \right]=\left[ -1.57,1.57 \right]$. We also know that range of $\sin x$ is $-1\le \sin x\le 1$. We now observe the curves of $\sin x$ and $x$ within the interval $\left[ -1.57,1.57 \right]$.

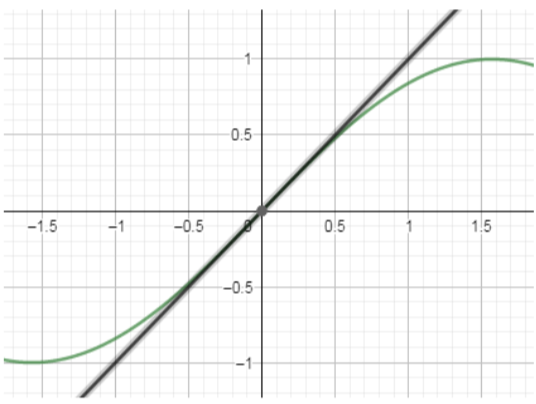
Let us find the left hand limit $\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]=\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{-x}{\sin \left( -x \right)} \right]$.When we see $x$ approaches to 0 from the left we have
     \[x<\sin x\Rightarrow -x>\sin \left( -x \right)\]
We see that from the left all the values of $x,\sin x$ are negative and negative of negative is positive. So now we divide the positive value and get.
\[x<\sin x\Rightarrow -x>\sin \left( -x \right)\Rightarrow \dfrac{-x}{\sin \left( -x \right)}>1\]. Then we have
\[\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]=\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{-x}{\sin \left( -x \right)} \right]=1\]
We can verify the values at two points of the interval from the left $\left[ \dfrac{-1.57}{\sin \left( -1.57 \right)} \right]=\left[ \dfrac{-1.57}{-1} \right]=1$ and $\left[ \dfrac{-0.01}{\sin \left( -0.01 \right)} \right]=\left[ \dfrac{-0.01}{-0.009} \right]=\left[ 1.11 \right]=1$\[\]
We can similarly find the right hand limit when $x$ approaches 0 from the right where $x>\sin x\Rightarrow \dfrac{x}{\sin x}>1$. Then we have
\[\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]=1\]
We can verify the values at two points of the interval from the right$\left[ \dfrac{1.57}{\sin \left( 1.57 \right)} \right]=\left[ \dfrac{1.57}{1} \right]=1$ and $\left[ \dfrac{0.01}{\sin \left( 0.01 \right)} \right]=\left[ \dfrac{0.01}{0.009} \right]=\left[ 1.11 \right]=1$\[\]
So the left hand limit is same as right hand limit and hence limit exists and the value is $\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]=1$
We find the limit of the other term in equation (1)
\[\underset{x\to 0}{\mathop{\lim }}\,{{x}^{x}}=\underset{x\to 0}{\mathop{\lim }}\,{{e}^{x\ln x}}=1\]
So the we get from equation(1)
\[\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+{{x}^{x}}=\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]+\underset{x\to 0}{\mathop{\lim }}\,{{x}^{x}}=1+1=2\]
So the correct choice is B.\[\]

Note: We can alternatively find the limit of $\underset{x\to 0}{\mathop{\lim }}\,\left[ \dfrac{x}{\sin x} \right]$ by replacing the denominator $\sin x$ with the sine series $\sin x=x-\dfrac{{{x}^{3}}}{3!}+\dfrac{{{x}^{5}}}{5!}+...$ . Then the term $x$ will cancel out in numerator and denominator when we take $x$ common in the sine series.