Question

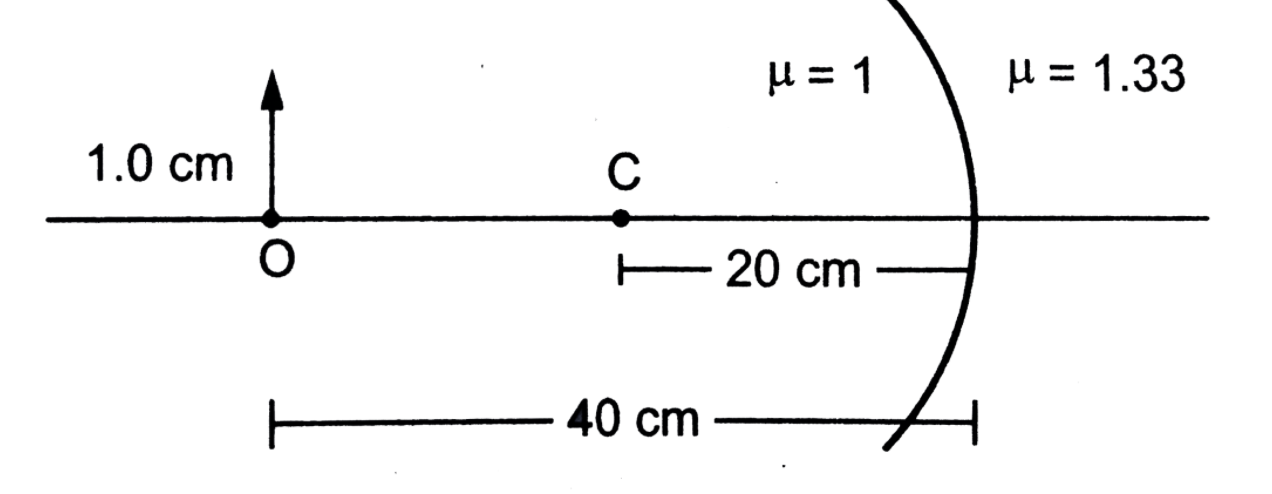
Find the size of the image formed in the situation shown in figure.

A) 0.5 cm
B) 0.6 cm
C) 1.2 cm
D) 1 cm

Answer 1

Hint: In this question, we have to find the size of the image and since all the required parameters are given in the question, we will find the required size of the image by mirror, we will use the mirror formula for two mediums.

Complete step by step answer:
We will now write the given data according to sign convention:
The distance of the object is u = -40 cm.
The radius of curvature of the refracting surface is R = -20 cm.
The height of the object is h = 1 cm.
We know that the lens maker formula is given by:
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
Here, v is the distance of image formed.
Here ${n_2} = 1.33$ is the refractive index of the second medium and ${n_1} = - 1$ is the refractive index of the first medium.
We will now substitute the known values in the above equation.
$\begin{array}{l}
\dfrac{{1.33}}{v} - \dfrac{1}{{ - 40\;cm}} = \dfrac{{1.33 - 1}}{{ - 20\;cm}}\\
v = 32.05\;cm
\end{array}$
We know that the expression for magnification ratio is given by:
$\dfrac{v}{u} = \dfrac{H}{h}$
Here, H is the height of the image formed.
We will now substitute the given and obtained values.
$\begin{array}{l}
 \Rightarrow \dfrac{{32.05\;cm}}{{40\;cm}} = \dfrac{H}{{1\;cm}}\\
 \Rightarrow H = 0.6\;cm
\end{array}$

Therefore, the correct option is (B).

Additional information: Reflection from a concave mirror follows the laws of reflection. The normal to the point of incidence is drawn along the radius of the mirror, i.e., it is drawn by joining the centre of curvature with the point of incidence.

Note: The formation of an image that occurs in a concave mirror mainly depends on the distance between the object and the mirror. Both real and virtual images are formed by the concave mirror. When the object is placed very close to the mirror, a virtual and magnified image is formed.