
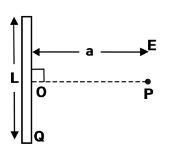
Find the electric field \[E\] at point \[P\] (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length \[L\] carrying a charge \[Q\]. The distance of the point \[P\] from the center of the rod is \[a = \left( {\frac{{\sqrt 3 }}{2}} \right)L\]
A. \[\frac{Q}{{2\sqrt 3 \pi {\varepsilon _o}{L^2}}}\]
B. \[\frac{{\sqrt 3 Q}}{{4\pi {\varepsilon _0}{L^2}}}\]
C. \[\frac{Q}{{3\pi {\varepsilon _o}{L^2}}}\]
D. \[\frac{Q}{{4\pi {\varepsilon _o}{L^2}}}\]
Answer
219.3k+ views
Hint: Write down the potential resulting from a point charge first. To determine the potential at point \[P\], integration on the line charge must be done. Therefore, choose a wire element \[\left( {dx} \right)\] and calculate its potential using the same methods as for a point charge.
Formula Used:
\[{{\rm{E}}_{{\rm{net }}}} = \frac{{{\rm{K}}\lambda }}{{\rm{r}}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)\]
Where \[{\theta _1},{\theta _2}\] are angle making with point \[{\rm{P}}\] from end.
Charge per unit length is \[\lambda \]
Complete answer:
We have been given in the question that,
Length of the wire \[ = L\]
Charge in the wire \[ = Q\]
Distance of the point \[P\] from the center of the rod is \[a = \left( {\frac{{\sqrt 3 }}{2}} \right)L\]
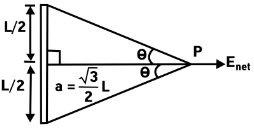
From the above diagram, we get
\[\tan \theta = \frac{{{\rm{ Perpendicular }}}}{{{\rm{ Base }}}}\]
Now, we have to observe the diagram and write the values in the above formula, we obtain\[\tan \theta = \frac{{\frac{L}{2}}}{{\frac{{\sqrt 3 }}{2}L}} = \frac{1}{{\sqrt 3 }}\]
On solving the above equation, we get
\[\theta = {30^\circ }\]
Now, we have to find electric field \[E\] at point \[P\]
Now,
\[{E_{net}} = \left( {\frac{{kQ}}{{\frac{{\sqrt 3 {L^2}}}{2}}}} \right)\left( {\sin {{30}^\circ } + \sin {{30}^\circ }} \right)\]
On solving the above equation by multiplying the terms inside the parentheses, we get
\[ = \left( {\frac{{2kQ}}{{\sqrt 3 {L^2}}}} \right)\left( {\frac{1}{2} + \frac{1}{2}} \right)\]
Now, we have to simplify the resultant equation, we have
\[ = \frac{1}{{4\pi {\varepsilon _0}}}\left( {\frac{{2Q}}{{\sqrt 3 {L^2}}}} \right)\]
On canceling the similar terms in the above expression, we get
\[ = \frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\]
Where: The net electric field is \[{\rm{E}}\].
The constant is \[{\rm{K}}\].
The charge in the wire is \[{\rm{Q}}\].
The wire's length is \[{\rm{L}}\].
Absolute permittivity is \[{\varepsilon _0}\].
Therefore, the electric field \[E\] at point \[P\] (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length \[L\] carrying a charge \[Q\] is \[\frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\].
Hence, the option A is correct.
Note: Students are likely to make mistake in these types of problems. In a brief, it can be claimed that because electric potential is a scalar number, it is zero at all points along the perpendicular bisector. The position of the force on a positive test charge is assumed to equal the position of the field.
Formula Used:
\[{{\rm{E}}_{{\rm{net }}}} = \frac{{{\rm{K}}\lambda }}{{\rm{r}}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)\]
Where \[{\theta _1},{\theta _2}\] are angle making with point \[{\rm{P}}\] from end.
Charge per unit length is \[\lambda \]
Complete answer:
We have been given in the question that,
Length of the wire \[ = L\]
Charge in the wire \[ = Q\]
Distance of the point \[P\] from the center of the rod is \[a = \left( {\frac{{\sqrt 3 }}{2}} \right)L\]

From the above diagram, we get
\[\tan \theta = \frac{{{\rm{ Perpendicular }}}}{{{\rm{ Base }}}}\]
Now, we have to observe the diagram and write the values in the above formula, we obtain\[\tan \theta = \frac{{\frac{L}{2}}}{{\frac{{\sqrt 3 }}{2}L}} = \frac{1}{{\sqrt 3 }}\]
On solving the above equation, we get
\[\theta = {30^\circ }\]
Now, we have to find electric field \[E\] at point \[P\]
Now,
\[{E_{net}} = \left( {\frac{{kQ}}{{\frac{{\sqrt 3 {L^2}}}{2}}}} \right)\left( {\sin {{30}^\circ } + \sin {{30}^\circ }} \right)\]
On solving the above equation by multiplying the terms inside the parentheses, we get
\[ = \left( {\frac{{2kQ}}{{\sqrt 3 {L^2}}}} \right)\left( {\frac{1}{2} + \frac{1}{2}} \right)\]
Now, we have to simplify the resultant equation, we have
\[ = \frac{1}{{4\pi {\varepsilon _0}}}\left( {\frac{{2Q}}{{\sqrt 3 {L^2}}}} \right)\]
On canceling the similar terms in the above expression, we get
\[ = \frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\]
Where: The net electric field is \[{\rm{E}}\].
The constant is \[{\rm{K}}\].
The charge in the wire is \[{\rm{Q}}\].
The wire's length is \[{\rm{L}}\].
Absolute permittivity is \[{\varepsilon _0}\].
Therefore, the electric field \[E\] at point \[P\] (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length \[L\] carrying a charge \[Q\] is \[\frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\].
Hence, the option A is correct.
Note: Students are likely to make mistake in these types of problems. In a brief, it can be claimed that because electric potential is a scalar number, it is zero at all points along the perpendicular bisector. The position of the force on a positive test charge is assumed to equal the position of the field.
Recently Updated Pages
Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

States of Matter Chapter For JEE Main Chemistry

Trending doubts
Understanding Uniform Acceleration in Physics

Understanding Atomic Structure for Beginners

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Average and RMS Value in Electrical Circuits

Other Pages
Understanding Entropy Changes in Different Processes

Common Ion Effect: Concept, Applications, and Problem-Solving

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

JEE Main 2025-26 Mock Test: Ultimate Practice Guide for Aspirants

Understanding Excess Pressure Inside a Liquid Drop

CBSE Class 10 Sanskrit Set 4 52 Question Paper 2025 – PDF, Solutions & Analysis




