Question

Find the capacitive time constant of the RC circuit shown in the figure.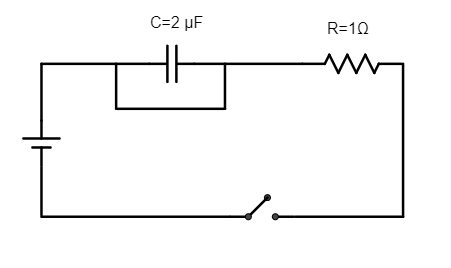

a) $0$
b) $\infty $
c) $2{\text{s}}$
d) $2\mu {\text{s}}$

Answer 1

Hint: The capacitor is shorted in the circuit diagram. This suggests that the potential difference across the capacitor is zero.

Formula Used: Time constant of the circuit is $\tau = RC$

Complete step by step answer:
Step 1: Explain the circuit diagram.

A capacitor of $C = 2\mu {\text{F}}$ is connected in series with a resistor of resistance $R = 1\Omega $ and connected to a battery. The capacitor is shorted.

Step 2: Determine the time constant of the circuit.

Time constant of the circuit is given by $\tau = RC$ .

Since the capacitor is shorted, the potential difference between the two plates will be zero.

We know that $C = \dfrac{Q}{V}$ .

Now, potential difference $V = 0$ .

This implies that $C = \infty $ .

Hence $\tau = R \times \infty = \infty $ .

Therefore, the correct option is b)$\infty $ .

Additional Information: When an increasing DC voltage is applied to a discharged capacitor, the capacitor charges up. When the voltage decreases the capacitor again discharges. This charging and discharging of the capacitor energy never happens in an instant. It takes some amount of time for the capacitor to charge or discharge to a specific percentage of its maximum supply value. This time is known as the time constant $\tau $. If the capacitor in the above RC circuit was not shorted, then the capacitor would have gradually charged up through the resistor until the voltage across the plates reached the supply voltage.

Note: Time constant represents the speed at which a system responds to change. Or, in this case it represents how fast the capacitor charges through the resistor. Here, the time constant is infinity. This means that the capacitor does not charge at all.