Question

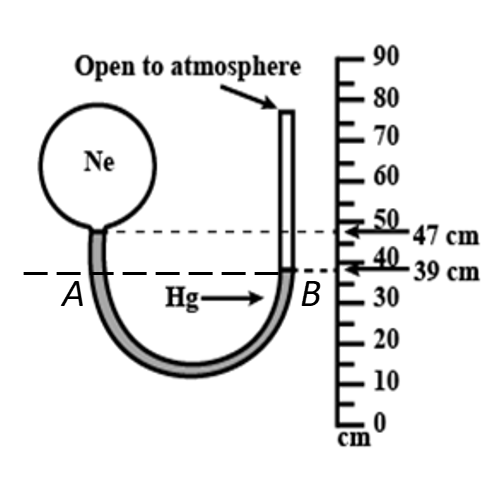
Find neon pressure in the manometer, when atmospheric pressure is 650 torr.

A) 665 torr
B) 80 torr
C) 570 torr
D) 650 torr

Answer 1

Hint: Manometer is a device that works on the principle of hydrostatic equilibrium. Hydrostatic equilibrium states that the pressure at any point in a fluid at rest is equal, and its value is just the weight of the overlying liquid.

Complete step by step answer:
Moving back to the question figure, we can see that height h of the manometric fluid column above point A is,
$h = 49\;{\rm{cm}} - 39\;{\rm{cm}}$
$ \Rightarrow h = 8\;{\rm{cm}} \times \dfrac{{10\;{\rm{mm}}}}{{1\;{\rm{cm}}}}$
$ \Rightarrow h = 80\;{\rm{mm}}$
Since point A and B are at the same levels, therefore the pressure at point A and B is the same, and it can be written as,
$ \Rightarrow {P_A} = {P_B}$
Now, the pressure at point A can also be written as the sum of the pressure of neon gas and the pressure to manometric fluid column h. Therefore,
$ \Rightarrow {P_{Ne}} + h = {P_A}$ …… (I)
Here ${P_{Ne}}$ is the pressure due to neon gas.
But since ${P_A} = {P_B}$ therefore the equation (I) becomes,
$ \Rightarrow {P_{Ne}} + h = {P_B}$ …… (II)
Since point B is open to atmosphere and therefore, the pressure at point B is equal to the atmospheric pressure, i.e. ${P_B} = 650\;{\rm{torr}}$.
We will now substitute ${P_B} = 650\;{\rm{torr}}$ and $h = 80\;{\rm{mm}}$ in equation (II), and therefore it becomes,
$ \Rightarrow {P_{Ne}} + 80\;{\rm{mm}} = 650\;{\rm{torr}} \times \dfrac{{1\;{\rm{mm}}}}{{1\;{\rm{torr}}}}$
$ \Rightarrow {P_{Ne}} + 80\;{\rm{mm}} = 650\;{\rm{mm}}$
$ \Rightarrow {P_{Ne}} = 570\;{\rm{mm}} \times \dfrac{{1\;{\rm{torr}}}}{{1\;{\rm{mm}}}}$
$ \Rightarrow {P_{Ne}} = 570\;{\rm{torr}}$

Therefore, the neon pressure in the manometer is 570 torr, and the correct option is (C).

Note: Since we have seen how a manometer is used, let us know some more applications of a manometer in daily life. In addition to straight pressure and vacuum measurement, other process variables that are a function of pressure can be readily measured with a manometer. Typical uses are flow, filter pressure drop, meter calibrations, leak testing and tank liquid level.