Question

Figure shows an irregular wedge of mass $m$ placed on a smooth horizontal surface. Horizontal part $BC$ is rough. The other part of the wedge is smooth. What minimum velocity should be imparted to a small block of same mass $m$ so that it may reach point $B$ .

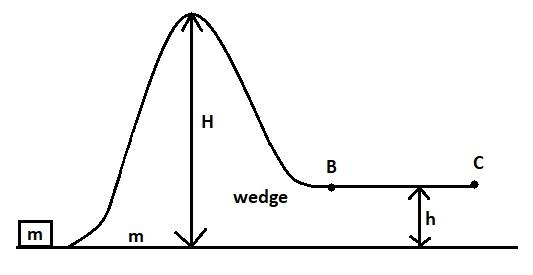
A) $2\sqrt {gH} $
B) $\sqrt {2gH} $
C) $2\sqrt {g\left( {H - h} \right)} $
D) $\sqrt {gH} $

Answer 1

Hint: For this we use the law of conservation of momentum which is momentum before and after collision is always conserved. And also use the equation of conservation of energy that energy is conserved before and after collision.

Complete step by step solution:
As we have a block of mass m move with initial velocity $\vec u$ and wedge with same mass m and initial velocity $\vec v$ .
Now according to the law of conservation of momentum: For a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision.
Therefore, $mu = \left( {m + m} \right)v$
Because after collision both the objects are combined so add their mass and they move with the same mass that is $m$ .
$ \Rightarrow mu = 2mv$
After calculating for $v$
$\therefore v = \dfrac{u}{2}$
After that we have an energy equation According to this total energy means potential and kinetic energy is equal before and after collision.
$\dfrac{1}{2}m{u^2} = mgH + \dfrac{1}{2}m{v^2} + \dfrac{1}{2}m{v^2}$
Because in starting only kinetic energy of block is in act whose velocity is $u$ and after that potential energy as well as kinetic energy of block and wedge is in act with common velocity $v$ .
$\dfrac{1}{2}m{u^2} = mgh + \dfrac{1}{2}m{\left( {\dfrac{u}{2}} \right)^2} + \dfrac{1}{2}m{\left( {\dfrac{u}{2}} \right)^2}$ (Insert value of $v$)
$\dfrac{1}{2}m{u^2} = mgh + \dfrac{1}{4}m{u^2}$
 Now, like terms should be on same side
$\dfrac{1}{2}m{u^2} - \dfrac{1}{4}m{u^2} = mgh$
After subtraction
$ \Rightarrow \dfrac{1}{4}m{u^2} = mgh$
By cancelling $m$ we have velocity which is equal to
${u^2} = 4gh$
$\therefore u = 2\sqrt {gh} $

So, Option (A) is correct.

Note: Always remember about kinetic energy and potential energy which one is come into action. Otherwise the answer will be wrong and also in momentum conservation law remember that $2\sqrt {gh} $ both objects combined and move with the same velocity.