Question

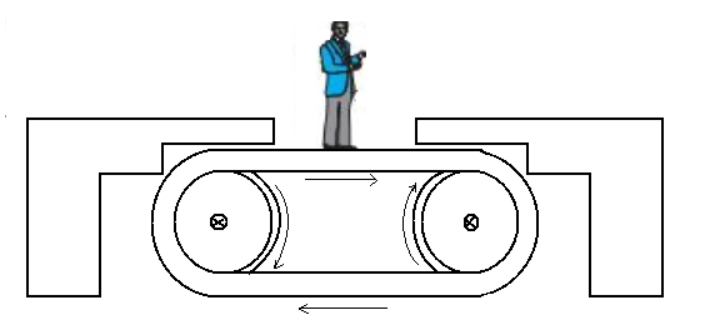
Figure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with $1\,m{s^{ - 2}}$. What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is $0.2$, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man $ = 65kg$ )

Answer 1

Hint: For the man to be at rest with respect to the conveyor belt his acceleration must be equal to the acceleration of the conveyor belt. The net force on the man will be given using Newton’s second law of motion; his mass multiplied by his acceleration. The maximum acceleration for which the man will be stationary relative to the belt can be calculated using the maximum static friction force acting on the man.

Complete step by step solution:
The man is given to be stationary with respect to the horizontal conveyor belt. For the man to be stationary the acceleration of the man must be equal to the acceleration of the conveyor belt.
The acceleration of the conveyor belt, ${a_c} = 1\,m{s^{ - 2}}$
Therefore, the acceleration of the man ${a_m}$ will be, \[{a_m} = {a_c} = 1\,m{s^{ - 2}}\]
This will be the acceleration of the man for which he will be stationary relative to the conveyor belt.
The net force on the man, using Newton’s second law will be: \[m{a_m}\] here, \[m\] is the mass of the man.
The mass of the man is given as, \[m = 65kg\]
Therefore, the net force on the man will be:
\[m{a_m} = 65 \times 1\]
\[ \Rightarrow m{a_m} = 65N\]
The net force on the man is \[65N\] . The man is at rest relative to the conveyor belt due to the frictional force acting between the man’s shoes and the belt.
The maximum value of frictional force \[f\] is given as:
\[f = \mu {\rm N}\]
Here, \[\mu \] is the coefficient of friction, it is given that \[\mu = 0.2\]

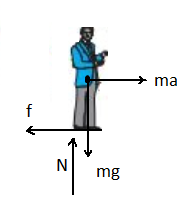
The normal force acting on the man is the reaction force between the man and the belt. This reaction force is balanced by the weight of the man which is given as:
\[{\rm N} = mg\]
Here, \[{\rm N}\] is the normal force and \[g\] is the acceleration due to gravity.
Substituting this value in \[f = \mu {\rm N}\] , we get
\[{f_{\max }} = m{a_{\max }} = \mu mg\]
Here, \[{f_{\max }}\] denotes maximum frictional force and \[{a_{\max }}\] denotes the maximum acceleration.
\[ \Rightarrow {a_{\max }} = \mu g\]
\[ \Rightarrow {a_{\max }} = 0.2 \times 10\] taking $g = 10m{s^{ - 2}}$
$ \Rightarrow a = 2m{s^{ - 2}}$
This is the maximum acceleration for which the man continues to be stationary relative to the belt.

Note: The man is relatively stationary due to the frictional force between the man’s shoes and the belt. This is similar to a person running on a cardio machine. The value of frictional force is limited and its maximum value is given as \[f = \mu {\rm N}\] . If the man moves with acceleration more than $2m{s^{ - 2}}$ , he will not be stationary and move in the forward direction.