Question

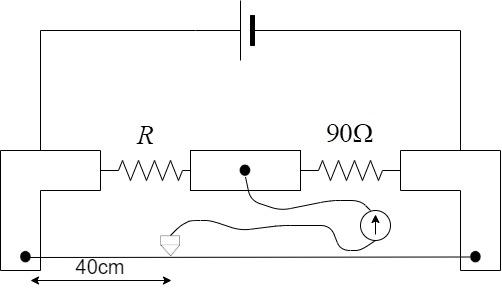
During an experiment with the metre bridge, the galvanometer shows a null point when the jockey is pressed at $40.0$ $cm$ using a standard resistance of $90\Omega $ as shown in the figure. The least count of the scale used in the meter bridge is 1mm. The unknown resistance is:

A) $60 \pm 0.15\Omega $
B) $135 \pm 0.56\Omega $
C) $60 \pm 0.25\Omega $
D) $135 \pm 0.23\Omega $

Answer 1

Hint: The Metre Bridge is an arrangement derived from the Wheatstone’s network. The Wheatstone’s network is an arrangement of 4 resistors as shown:

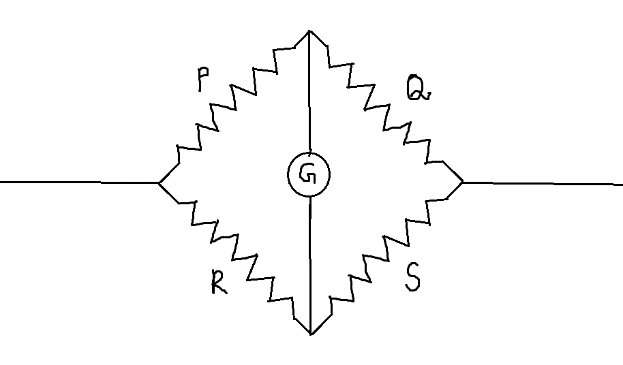
The Wheatstone’s network is said to be balanced if the reading in the galvanometer becomes zero. This condition is possible when –
$\dfrac{P}{Q} = \dfrac{R}{S}$

Complete step by step answer:
Step 1: Calculating the unknown resistance.
In a meter bridge, the ratio of the known resistance to the unknown resistance is equal to the ratio of the corresponding lengths.
If the galvanometer reading turns 0 when the jockey is pressed at a length $l$, the formula for finding the unknown resistance R –
$\dfrac{R}{S} = \dfrac{l}{{1 - l}}$
where S – known resistance.
In this problem,
$
\Rightarrow S = 90\Omega \\
\Rightarrow l = 40cm = 0.4m \\
 $
Hence, substitute these values to obtain the unknown resistance R –
$
\Rightarrow \dfrac{R}{S} = \dfrac{l}{{1 - l}} \\
\Rightarrow R = S\dfrac{l}{{1 - l}} \\
  Solving, \\
\Rightarrow R = 90\dfrac{{0.4}}{{1 - 0.4}} \\
\Rightarrow R = 90\dfrac{{0.4}}{{0.6}} = 60\Omega \\
 $

Step 2: Finding the change in resistance
Let us consider the equation for unknown resistance in the meter bridge
$R = S\dfrac{l}{{1 - l}}$
To find the incremental value of change in resistance, we need to differentiate the equation with respect to length
$
\Rightarrow \dfrac{{dR}}{{dl}} = R\left( {\dfrac{1}{l} + \dfrac{1}{{1 - l}}} \right) \\
  rearranging, \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
 $
Least count,$dl = 1mm = 0.001m$
Substituting in the formula, we get:
$
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{dl}}{l} + \dfrac{{dl}}{{1 - l}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{1 - 0.4}} \\
\Rightarrow \dfrac{{dR}}{R} = \dfrac{{0.001}}{{0.4}} + \dfrac{{0.001}}{{0.6}} = \dfrac{{0.01}}{4} + \dfrac{{0.01}}{6} \\
\Rightarrow \dfrac{{dR}}{R} = 0.25\Omega \\
 $
Hence, incremental change = $ \pm 0.25\Omega $

Hence, the correct option is Option C, $60 \pm 0.25\Omega.$

Note: Students can, often, get confused between R and S in the formula. Always, note that the known resistance will be in the denominator as it is connected on the left. So, the known resistance S will be equivalent to (1-l).