Question

Drops of water fall from the roof of a building $9m$ high at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distances of the second and third drops from the roof?
(A) $6m$ and $2m$
(B) $6m$ and $3m$
(C) $4m$ and $1m$
(D) $4m$ and $2m$

Answer 1

Hint: Since the drops fall at a regular interval of time, the time taken by all of the drops to reach the ground will be the same. If the first drop reaches the ground at the same time when the fourth drop starts to fall then the time taken by this drop can be assumed to be four times of a uniform time interval. This could be put into the equations of motion, which gives the required quantities.

Complete step by step answer: When the first drop reaches the ground, the fourth drop starts to fall, this means that by the time the first drop reaches the ground, three more drops have formed. The time taken by the first drop to reach the ground is $3t$.
Where $t$ is the time taken by each drop to get generated.

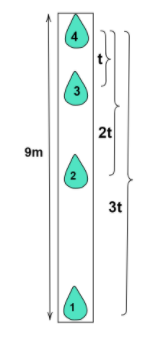
The height of the roof from which the drops fall is given as $h = 9m$
It is known that the drops fall under the action of gravity. Thus the acceleration of the drops would be taken as $g = 10m/{s^2}$
For the first drop,
We have the initial velocity of drop 1, $u = 0$
Putting these values in the second equation of motion,
$s = ut + \dfrac{1}{2}a{t^2}$
$ \Rightarrow 9 = 0 \times 3t + \dfrac{1}{2} \times 10{(3t)^2}$
$ \Rightarrow 9{t^2} = 1.8$
$ \Rightarrow {t^2} = 0.2$
$ \Rightarrow t = \sqrt {0.2} $seconds..
We get the time interval between the releasing of each drop as $t = 1.8\sec $.
Now to calculate the distance travelled by the second drop-
The second drop takes a time interval equal to $2t$to cover this given distance.
Putting these values in the equation of motion again,
We have-
$s = ut + \dfrac{1}{2}a{t^2}$
$ \Rightarrow {s_2} = 0 \times {\kern 1pt} \sqrt {0.2} + \dfrac{1}{2} \times 10 \times {\left( {2 \times \sqrt {0.2} } \right)^2}$
$ \Rightarrow s = 5 \times 4 \times 0.2 = 4$
The distance covered by the second drop is,${s_2} = 4m$
To calculate the distance travelled by the third drop-
The third drop takes a time interval equal to $t$to cover the given distance.
We have,
$s = ut + \dfrac{1}{2}a{t^2}$
\[ \Rightarrow {s_3} = 0 \times \sqrt {0.2} + \dfrac{1}{2} \times 10 \times {\left( {\sqrt {0.2} } \right)^2}\]
\[ \Rightarrow {s_3} = 5 \times 0.2 = 1\]
The distance covered by the third drop is, \[{s_3} = 1\]

Therefore the option, (C) is correct.

Note: It is given that the time taken by all drops to reach the ground is the same. But this does not imply that the distance covered by them in each second is also the same. Since the gravitational force causes the acceleration, the distance covered in each second is more than the previous second.