Question

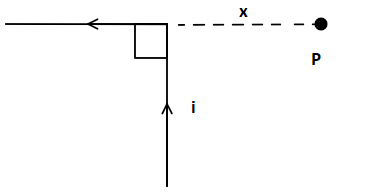
Determine the magnetic field at point P located at a distance \[x\] from the corner of an infinitely long straight conductor bent at right angle as shown in the figure. The wire carries a steady current $i$.

Answer 1

Hint: Determining magnetic field at a point means to determine the magnitude and direction of magnetic field at that point. In this case the magnetic field is due to the infinitely long wire or we can assume it is due to two infinitely long conductors carrying the same amount of current.

Complete step by step solution:
Let’s start with the position of the point P with respect to the infinitely long wire. At the point of bending of the conductor we can assume that there are two conductors suspending angles $0^\circ $ and $90^\circ $ respectively towards the ends of the conductor.
As per Biot-Savarts’ law we know that the magnetic field intensity at a point due to a straight current carrying wire is,
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}(\sin {\phi _1} + \sin {\phi _2})$
Where $B$ is the magnetic field intensity
$I$ is the steady current flowing through the infinitely long conductor
$r$ is the distance of the point where magnetic field is being calculated from the wire
${\phi _1}$ and ${\phi _2}$ are the angles suspended by the ends of the conductor at the point of concern
From the figure given in the question we can say that the point P is at angles $0^\circ $ and $90^\circ $ from the both ends of the conductor. The assumption of two conductors was made for ease of understanding.
We are given that the point P is at a distance \[x\] from the conductor.
Substituting these values we get,
$ \Rightarrow B = \dfrac{{{\mu _0}i}}{{4\pi x}}(\sin 90^\circ + \sin 0^\circ )$
$ \Rightarrow B = \dfrac{{{\mu _0}i}}{{4\pi x}}$
This is the magnitude of the magnetic field at the point P for the straight current carrying conductor of infinite length.
Now for the direction of the magnetic field we can use the right hand thumb rule.
By doing so, we get that its direction is perpendicular to the plane of paper and directed inwards.

Note:Make sure to estimate the direction of the magnetic field as students often forget about the direction part and only calculate the magnitude. In the right hand thumb rule the direction of thumb is for the direction of current and other fingers point towards the direction of magnetic field. The principle of Biot-Savarts’ law is applied for solving this problem.