Question

Current of 10 amperes and 2 amperes are passed through two parallel wires A and B, respectively in opposite directions. If the wire A is infinitely long and the length of the wire B is 2m, the force on the conductor B which is situated at 10cm distance from A will be:
A) $8 \times {10^{ - 5}}N$
B) $4 \times {10^{ - 5}}N$
C) $8\pi \times {10^{ - 5}}N$
D) $4\pi \times {10^{ - 5}}N$

Answer 1

Hint: To solve this question, the concept that needs to be applied is – whenever a current carrying conductor is placed in an external magnetic field, there is a force applied in the direction perpendicular to the direction of the magnetic field and the current.

Complete step by step answer:
Consider 2 wires A and B running parallely with wire A being infinitely long and length of wire being 2m.

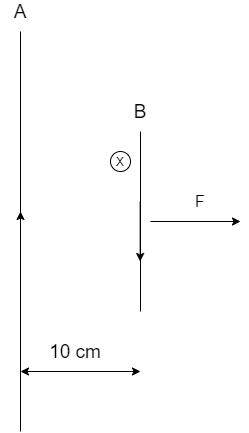
Here, the force is exerted on the conductor B due to the magnetic field produced by the current carrying wire A.
The direction of magnetic field from the wire A can be calculated by the Right-Hand thumb rule which states that – If the thumb of the right hand is oriented towards the direction of current, the direction of curl of the other four fingers indicates the direction of the induced magnetic field.
In this figure, by applying the rule, we see that the magnetic field is going inside the plane of the paper and denoted by X in the figure.
The magnetic field induced is given by the formula:
$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2{I_A}}}{d}$
where
$\dfrac{{{\mu _0}}}{{4\pi }}$ = constant value representing the magnetic permeability, whose value is equal to ${10^{ - 7}}$.
Given,
Current in the wire A, ${I_A} = 10A$
Distance of separation, $d = 10cm = 0 \cdot 1m$
Substituting, we get –
$B = {10^{ - 7}} \times \dfrac{{2 \times 10}}{{0 \cdot 1}} = 200 \times {10^{ - 7}}T$
The force acting on the wire B due to the magnetic field by wire A is given by –
$F = BIL$
where B = magnetic field, I = current and L = length.
Current in wire B, ${I_B} = 2A$
Length of the wire, $L = 2m$
Substituting, we get –
$F = BIL = 200 \times {10^{ - 7}} \times 2 \times 2 = 800 \times {10^{ - 7}} = 8 \times {10^{ - 5}}N$

Hence, the correct option is Option A.

Note: The direction of the force on the conductor B as seen in the figure is away from the conductor A. This is obtained by applying the Fleming’s Left Hand rule which states that – If the index, middle and thumb fingers of the left hand are held in mutually perpendicular directions and, the index finger and the middle finger of the left hand indicate the direction of magnetic field and current respectively, the force is represented by the thumb.