Question

Consider the following reactions \[{\rm{A}} \to {{\rm{P}}_{\rm{1}}}{\rm{;B}} \to {{\rm{P}}_{\rm{2}}}{\rm{;C}} \to {{\rm{P}}_{\rm{3}}}{\rm{;D}} \to {{\rm{P}}_{\rm{4}}},\]
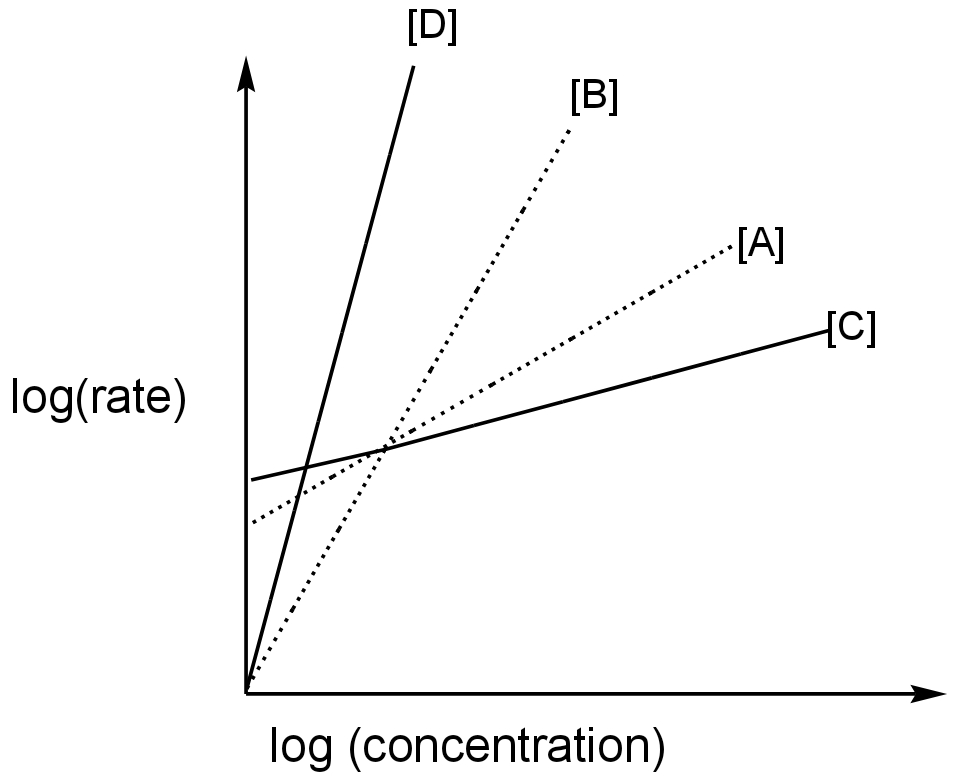
The order of the above reactions is a,b,c, and d, respectively. The following graph is obtained when log[rate] vs. log[conc.] are plotted.

Among the following the correct sequence for the order of the reactions is:
A. c > a > b > d
B. d > a > b > c
C. d > b > a > c
D. a > b > c > d

Answer 1

Hint: We are given a graph of four reactions plotted log(rate) against log(concentration). To find which reaction has a higher-order, we have to compare the slope of each reaction.

Formula Used:
\[{\rm{log(rate) = nlog(concentration) + logk}}\]

Complete Step by Step Solution:
In this graph log(rate) is plotted against log(concentration).
The graph is linear for all four reactions.

It means the rate changes with the concentration of the reactant.
Rate is directly proportional to the concentration of the reactant.

Let us consider the order of the reactions to be n.
\[{\rm{Rate = k[A}}{{\rm{]}}^{\rm{n}}}\] for the first reaction.
\[{\rm{Rate = k[B}}{{\rm{]}}^{\rm{n}}}\]for the second reaction.
\[{\rm{Rate = k[C}}{{\rm{]}}^{\rm{n}}}\]for the third reaction.
\[{\rm{Rate = k[D}}{{\rm{]}}^{\rm{n}}}\]for the fourth reaction.

If we take the log for a rate law equation we get
\[{\rm{Rate = k(concentration}}{{\rm{)}}^{\rm{n}}}\]
\[{\rm{log(rate) = nlog(concentration) + logk}}\]

This equation resembles the mathematical expression \[{\rm{y = mx + c}}\].

Thus, comparing both the equations we get,
Slope or m is the order of the reaction.
Thus, the reaction having more slope will have more order.

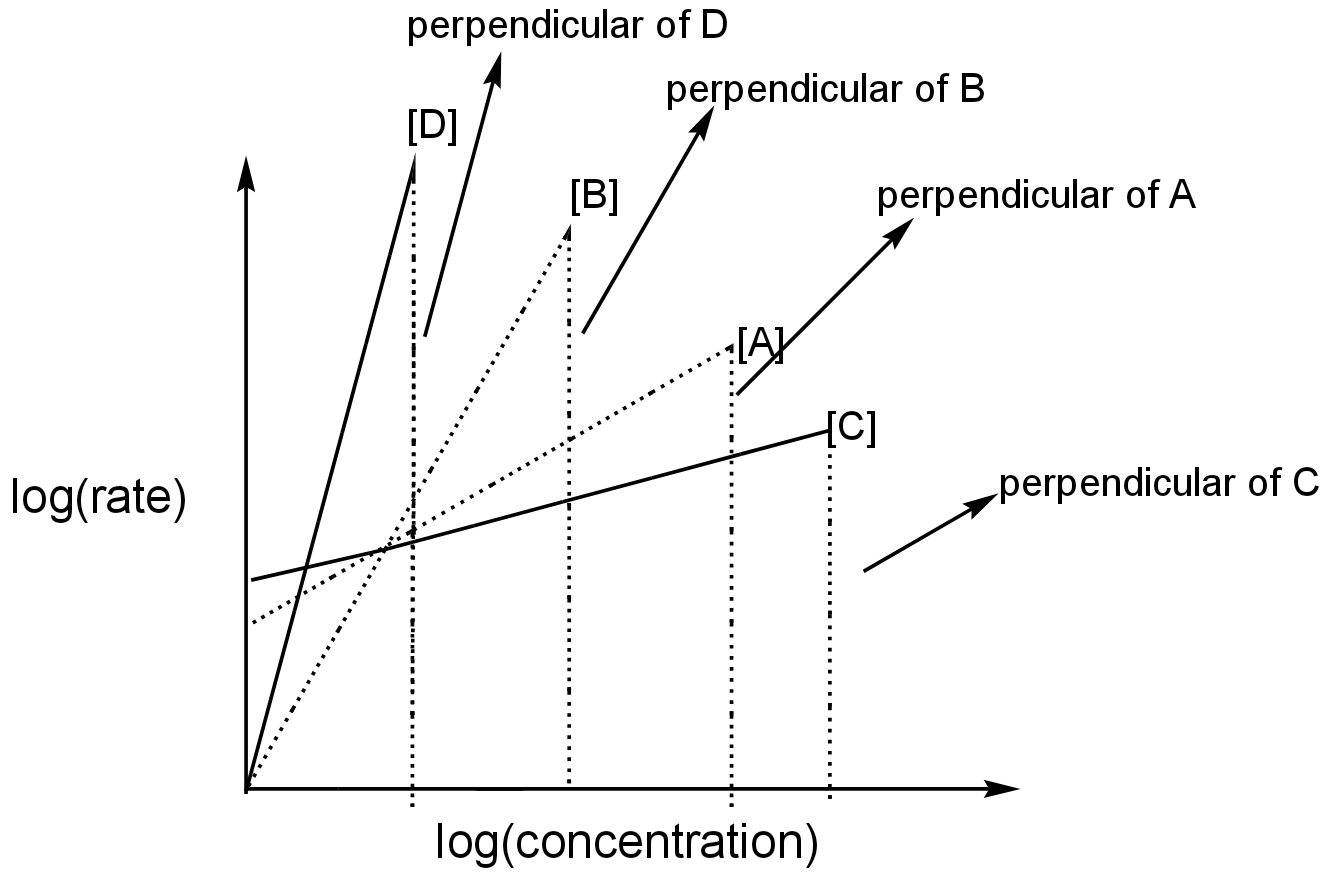
Image: perpendiculars of the slopes of different reactions.

The line which has a higher length of perpendicular has a higher slope.
D has the highest length of perpendicular, so has the highest slope and hence, the highest order.
B has a perpendicular less than D but more than A and C.
A has a higher length of perpendicular than C.
C has the least length of perpendicular as compared to others. Hence, C has the lowest order.

Thus, the correct sequence for the order of the reactions is d>b>a>c

So, option C is correct.

Note: We know that the tangent of an angle gives the slope. The tangent of an angle is the ratio of its perpendicular to the base. So, if the line has a higher length perpendicular, then it will have more slope. So, by observing the graph we can see whose perpendicular has a higher length and higher slope.