Answer
64.8k+ views
Hint: The minimum distance between the Sun and the body will be when the body velocity is perpendicular to its position vector relative to the Sun.
Complete step by step answer:
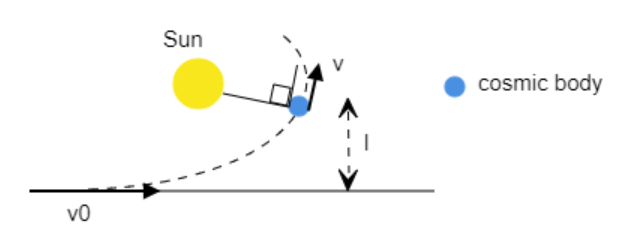
Step 1: Sketch an appropriate figure and mark the point of minimum distance between the Sun and the body.
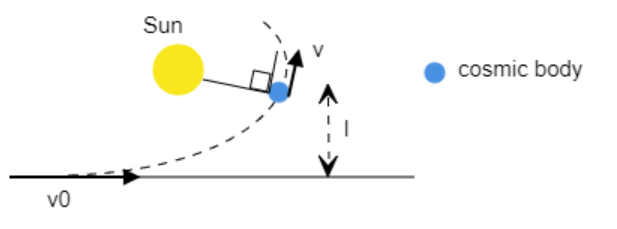
Step 2: Use conservation of angular momentum to obtain an expression for the velocity of the body when it is at a minimum distance to the Sun.
Step 3: Use conservation of energy to find the minimum distance ${r_{\min }}$ between the sun and the body.
Step 4: The above equation is a quadratic equation in ${r_{\min }}$. Roots of the equation can be obtained using the quadratic formula.
We have, ${v_0}^2{r_{\min }}^2 + 2GM{r_{\min }} - {v_0}^2{l^2} = 0$ is same as $a{x^2} + bx + c = 0$.
Here, $x = {r_{\min }}{\text{, }}a = {v_0}^2{\text{, }}b = 2GM{\text{ and }}c = - {v_0}^2{l^2}$.
Applying the quadratic formula, ${r_{\min }} = \dfrac{{ - 2GM \pm \sqrt {4{G^2}{M^2} + 4{v_0}^4{l^2}} }}{{2{v_0}^2}}$.
Simplifying we get, ${r_{\min }} = \dfrac{{ - 2GM}}{{2{v_0}^2}} \pm \dfrac{1}{{2{v_0}^2}}\sqrt {4{G^2}{M^2}\left( {1 + \dfrac{{{v_0}^2{l^2}}}{{{G^2}{M^2}}}} \right)} $.
Note: The motion of the cosmic body is angular or rotational as shown in the figure. Thus, angular momentum is the term of interest as the relation for angular momentum involves the distance $r$ from the rotational axis. Here this distance is the distance between the Sun and the cosmic body. Once the roots of ${r_{\min }}$ (positive and negative) are obtained, we consider the positive root of ${r_{\min }}$ as it is a measure of distance and distance must not be a negative value.
Complete step by step answer:
Step 1: Sketch an appropriate figure and mark the point of minimum distance between the Sun and the body.

Step 2: Use conservation of angular momentum to obtain an expression for the velocity of the body when it is at a minimum distance to the Sun.
The body moves with an initial velocity ${v_0}$ from point A to point B. At point B, the body’ s velocity $v$ is perpendicular to its position vector relative to the Sun and thus at point B, minimum distance ${r_{min}}$ exists between the Sun and the body.
At both points A and B, the angular momentum must be conserved.
By conservation of angular momentum, we have ${L_A} = {L_B}$.
Angular momentum at A is ${L_A} = l \times m{v_0} = m{v_0}l\sin \theta $
where, $m{v_0}$ is the linear momentum and $l$ is the distance from the rotation axis.
Since, $l$ is assumed to be perpendicular to the body’s linear momentum $(\theta = 0)$
we have the angular momentum at A as, ${L_A} = m{v_0}l$.
Angular momentum at B is ${L_B} = {r_{\min }} \times mv = mv{r_{\min }}$
where, $mv$ is the linear momentum at B and ${r_{min}}$ is the distance from the rotation axis. At B, ${r_{\min }}$ is perpendicular to the velocity v (and linear momentum).
Rearranging the above equation, we get, $v = \dfrac{{{v_0}l}}{{{r_{\min }}}}$.
Step 3: Use conservation of energy to find the minimum distance ${r_{\min }}$ between the sun and the body.
According to the conservation of energy, the total energy at A (sum of the potential energy and kinetic energy of the body) must equal the total energy at B.
At A, potential energy of the body is zero since it is far away from the Sun.
At A, kinetic energy of the body at A is $\dfrac{1}{2}m{v_0}^2$.
At B, gravitational potential energy exists and is given by, $\dfrac{{ - GMm}}{{{r_{\min }}}}$ where $G$is the gravitational constant, $M$ is the mass of the Sun, $m$ is the mass of the body and ${r_{\min }}$ is the distance between the Sun and the body.
At B, the kinetic energy is given as $\dfrac{1}{2}m{v^2}$.
By conservation of energy, $\dfrac{1}{2}m{v_0}^2 = \dfrac{1}{2}m{v^2} - \dfrac{{GMm}}{{{r_{\min }}}}$.
On simplifying we get, $\dfrac{{{v^2}}}{2} - \dfrac{{{v_0}^2}}{2} = \dfrac{{GM}}{{{r_{\min }}}}$.
Substitute for $v = \dfrac{{{v_0}l}}{{{r_{\min }}}}$ in the above equation and then rearranging, $\dfrac{{{v_0}^2}}{2} = \dfrac{{{v_0}^2{l^2}}}{{2{r_{\min }}^2}} - \dfrac{{GM}}{{{r_{\min }}}}$.
Multiply throughout by $2{r_{\min }}^2$ to get a quadratic equation in ${r_{\min }}$.
i.e., ${v_0}^2{r_{\min }}^2 = {v_0}^2{l^2} - 2GM{r_{\min }}$ or ${v_0}^2{r_{\min }}^2 + 2GM{r_{\min }} - {v_0}^2{l^2} = 0$.
Step 4: The above equation is a quadratic equation in ${r_{\min }}$. Roots of the equation can be obtained using the quadratic formula.
We have, ${v_0}^2{r_{\min }}^2 + 2GM{r_{\min }} - {v_0}^2{l^2} = 0$ is same as $a{x^2} + bx + c = 0$.
Here, $x = {r_{\min }}{\text{, }}a = {v_0}^2{\text{, }}b = 2GM{\text{ and }}c = - {v_0}^2{l^2}$.
Applying the quadratic formula, ${r_{\min }} = \dfrac{{ - 2GM \pm \sqrt {4{G^2}{M^2} + 4{v_0}^4{l^2}} }}{{2{v_0}^2}}$.
Simplifying we get, ${r_{\min }} = \dfrac{{ - 2GM}}{{2{v_0}^2}} \pm \dfrac{1}{{2{v_0}^2}}\sqrt {4{G^2}{M^2}\left( {1 + \dfrac{{{v_0}^2{l^2}}}{{{G^2}{M^2}}}} \right)} $.
Cancel the common terms in numerator and denominator to get, ${r_{\min }} = \dfrac{{ - GM}}{{{v_0}^2}} \pm \dfrac{{GM}}{{{v_0}^2}}\sqrt {\left( {1 + \dfrac{{{v_0}^2{l^2}}}{{{G^2}{M^2}}}} \right)} $.
Taking $\dfrac{{GM}}{{{v_0}^2}}$ from the terms, we have
${r_{\min }} = \dfrac{{GM}}{{{v_0}^2}}\left[ { - 1 \pm \left( {\sqrt {\left( {1 + \dfrac{{{v_0}^2{l^2}}}{{{G^2}{M^2}}}} \right)} } \right)} \right]$.
We only take the positive root of ${r_{\min }}$.
i.e., we have ${r_{\min }} = \dfrac{{GM}}{{{v_0}^2}}\left[ {\sqrt {\left( {1 + \dfrac{{{v_0}^2{l^2}}}{{{G^2}{M^2}}}} \right)} - 1} \right]$.
Note: The motion of the cosmic body is angular or rotational as shown in the figure. Thus, angular momentum is the term of interest as the relation for angular momentum involves the distance $r$ from the rotational axis. Here this distance is the distance between the Sun and the cosmic body. Once the roots of ${r_{\min }}$ (positive and negative) are obtained, we consider the positive root of ${r_{\min }}$ as it is a measure of distance and distance must not be a negative value.
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

What is the common property of the oxides CONO and class 10 chemistry JEE_Main

What happens when dilute hydrochloric acid is added class 10 chemistry JEE_Main

If four points A63B 35C4 2 and Dx3x are given in such class 10 maths JEE_Main

The area of square inscribed in a circle of diameter class 10 maths JEE_Main